Question

A rectangular parking lot is 50ft longer than it is wide. How do you determine the dimensions of the parking lot if it measures 250ft diagonally?

Answer 1

In this problem, we have to find the dimensions, i.e. length and width of the parking lot with the given data. We can see that the length is 50ft longer than its width. We can also see that we have a diagonal of 250ft in the rectangular parking lot, so we can use Pythagoras theorem so that we will get a quadratic equation from which we can find the width and the length.

Complete step by step solution:
We can assume that,
Let the length be L.
Let the width be W.
We know that, we are given a rectangular parking lot is 50ft longer than it is wide,
$L=W+50$…… (1)
Now we can draw the diagram.

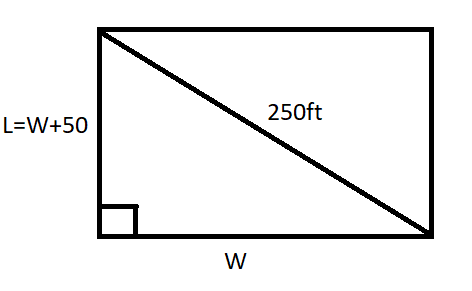
We can now use the Pythagoras theorem.
${{L}^{2}}+{{W}^{2}}={{\left( 250 \right)}^{2}}$
We can substitute the value of (1) in the above formula we get
${{\left( W+50 \right)}^{2}}+{{W}^{2}}={{\left( 250 \right)}^{2}}$
Now we can simplify it using whole square formula, we get
$\Rightarrow {{W}^{2}}+100W+2500+{{W}^{2}}={{250}^{2}}$
Now we can simplify the above step, we get
$\Rightarrow 2{{W}^{2}}+100W-60000=0$
We can now divide by 2 in the above step, we get
$\Rightarrow {{W}^{2}}+50W-30000=0$
We can now use the quadratic formula for the equation $a{{x}^{2}}+bx+c=0$.
Where, a = 1, b = 50, c = -30000.
$W=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
We can substitute the values, we get

& \Rightarrow W=\dfrac{-50\pm \sqrt{{{50}^{2}}-4\left( -30000 \right)}}{2} \\\ & \Rightarrow W=\dfrac{-50\pm 350}{2} \\\ & \Rightarrow W=-200,150 \\\ \end{aligned}$$ We know that -200 cannot be the width. Therefore, the width is 150ft. We can substitute the width value in (1), we get $$L=150+50=200$$ **Therefore, the length of the parking lot is 200ft and the width of the parking lot is 150ft.** **Note:** Students make mistakes while calculating the width using the quadratic formula by substituting the values. We should also know the Pythagoras theorem to solve these types of problems. We should go through the question carefully to understand the given data exactly.