Question

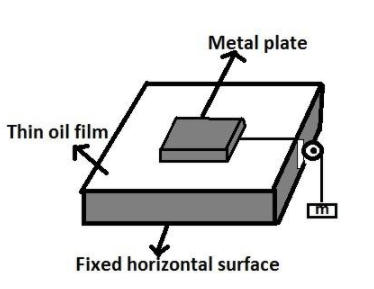
A rectangular metal plate has dimensions of 10 cm × 20 cm. A thin film of oil separates the plate from a fixed horizontal surface. The separation between the rectangular plate and the horizontal surface is $0.2mm$. An ideal string is attached to the plate and passes over an ideal pulley to a mass m. When m = 125 g, the metal plate moves at constant speed of $5cm/s$ across the horizontal surface. Then the coefficient of viscosity of oil in $dyne - cm/{s^2}$ is:
(Use $g = 1000cm/{s^2}$)

(A) 5
(B) 2.5
(C) 25
(D) 30

Answer 1

The viscous force is proportional to the coefficient of viscosity, area and velocity gradient. The weight of the block is equal to the viscous force when the block moves with a constant velocity.
Formula Used: The formulae used in the solution are given here.
Viscous force is can be expressed as ${F_{viscous}} = \eta A\dfrac{{dV}}{{dx}}$ where $\eta$ is the coefficient of viscosity, $A$ is the area and $\dfrac{{dV}}{{dx}}$ is the rate of change of velocity with respect to distance.

Complete Step by Step Solution: Viscosity is defined as the degree up to which a fluid resists the flow under an applied force; it is measured by the tangential friction force acting per unit area divided by the velocity gradient under conditions of streamline flow.
The viscosity is calculated in terms of the coefficient of viscosity. It is constant for a liquid and depends on its liquid’s nature. The coefficient of viscosity is the ratio of tangential stress on the top surface of film (exerted by block) to that of velocity gradient (vertically downwards) of film.
It has been given that a rectangular metal plate has dimensions of 10 cm × 20 cm and is separated from a fixed horizontal surface by a thin film of oil. The separation between the rectangular plate and the horizontal surface is $0.2mm$.
An ideal string is attached to the plate and passes over an ideal pulley to a mass $m$. When $m = 125g$, the metal plate moves at constant speed of $5cm/s$ across the horizontal surface.
Viscous force is can be expressed as ${F_{viscous}} = \eta A\dfrac{{dV}}{{dx}}$ where $\eta$ is the coefficient of viscosity, $A$ is the area and $\dfrac{{dV}}{{dx}}$ is the rate of change of velocity with respect to distance.
It is also known as the velocity gradient.
Given that, velocity $V = 5cm/s$ and the separation between the rectangular plate and the horizontal surface is $x$, when $x = 0.2mm$.
Thus, assigning the values, the velocity gradient is,
$\dfrac{{dV}}{{dx}} = \dfrac{5}{{0.02}} = 250mm$.
The weight of the block is equal to the viscous force when the block moves with a constant velocity.
Thus,
$weight = mg = 125 \times 1000$
$= 125000g - dyne - cm/{s^2}$
Thus, the viscous force is ${F_{viscous}} = 125000g - dyne - cm/{s^2}$
Given the rectangular plate has dimensions of 10 cm × 20 cm. This is the area.
Now the coefficient of viscosity given by, assigning the values,
$\eta = \dfrac{{125 \times 1000}}{{10 \times 20}}.\dfrac{1}{{250}}$
$\Rightarrow \eta = 2.5dyne - s/c{m^{ - 2}}$

Hence, the correct answer is Option B.

Note: The coefficient of viscosity of fluids will be decreased as the temperature increases, while it is inverse in the case of gases. While the coefficient of viscosity of gases will increase with the increase in temperature. The increase in temperature for the fluid deliberate the bonds between molecules. These bonds are directly associated with the viscosity and finally, the coefficient is decreased.