Question

A rectangular loop with a sliding connector of $length = 1.0\,m$ is situated in a uniform magnetic field $field = 2t$ perpendicular to the plane of loop. Resistance of the connector is $r = 2\Omega$ . Two resistance is $6\Omega$ and $3\Omega$ are connected as shown in the figure. The external force required to keep the connector moving with a constant velocity $v = 2m{s^{ - 1}}$

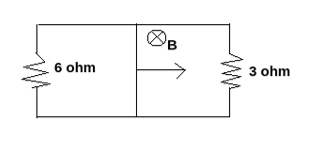
(A) $6N$
(B) $4N$
(C) $2N$
(D) $1N$

Answer 1

Hint Uniform magnetic field: it is a kind of magnetic field that has the same magnitude and direction throughout the region which is under observation, thus the field line needs to be both parallel and space out evenly. Induced EMF: emf which is generated due to change in the magnetic flux is known as induced emf. Emf stands for electromotive force. $E = vBl$ . Magnetic force is the force of attraction or repulsion that comes into picture due to motion of electric charged particles $F = ilB$ .

Step-by-step solution
Given that, the resistance of the connector $2\Omega$
magnetic field - $2t$
two resistance - $6\Omega$ and $3\Omega$
velocity of moving connector - $2m{s^{ - 1}}$
Let’s calculate the induced emf generated in the circuit.
$E = vBl$
$E = 2 \times 2 \times 1$
$E = 4V$
Now, consider the two resistances $6\Omega$ and $3\Omega$ since they are in parallel connected then the resultant resistance will be $2\Omega$
So, now by considering the above findings we can have a figure as shown below

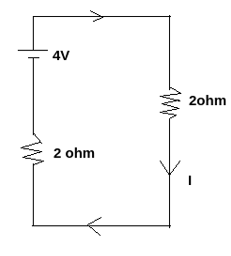
With the help of above diagram, we can easily find the value of $I$ (current) which is flowing through the circuit which is $I = \dfrac{4}{{2 + 2}}$ which will give us the value $1\,ampere$ is flowing in clockwise direction.
Now, calculation the magnetic force on connector by using formula $F = ilB$
$F = 1 \times 1 \times 2$
$\Rightarrow F = 2N$
The direction of this force is towards the left.
So, as a result if we want to move our connector with a constant velocity, we need to apply force of $2N$

Therefore, option (a) will be the correct answer.

Note always try to go approach step by step otherwise questions like this can confuse a bit. Also, try to remember the formulas of electromotive force $E = vBl$ , magnetic force $F = ilB$ and also the formula to find the resultant of connected resistances for series connection formula will be $R = {r_1} + {r_2} + ... + {r_n}$ .