Question

A rectangular loop with a sliding connector $CD$ of length $l=1.0\,m$ is situated in uniform and constant magnetic field $B=2\,T$ perpendicular to the plane of loop. Resistance of connector $CD$ is $r=2\,\Omega$. Two resistances of $6\,\Omega$ and $3\,\Omega$ are connected as shown in figure. The external force required to keep the connector moving with a constant velocity $v=2\,m/s$ perpendicular to $CD$ and in the plane of the loop is:

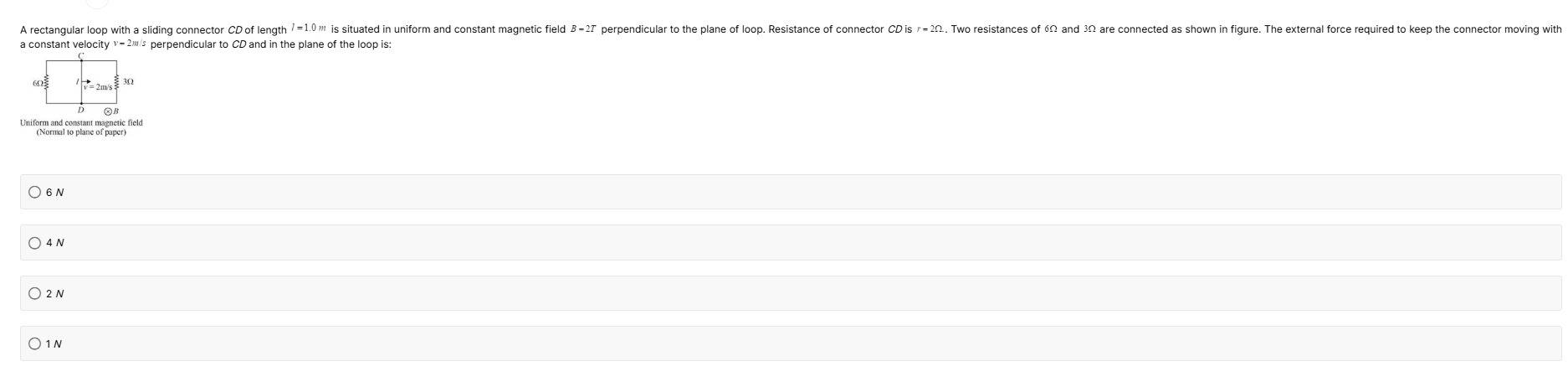
• A. 6 N
• B. 4 N
• C. 2 N
• D. 1 N

Answer 1

Answer: (C)

2 N

Answer 2

1. Calculate the induced EMF in the sliding conductor $CD$ using $E = Blv$. $E = (2\,T)(1.0\,m)(2\,m/s) = 4\,V$.

2. Calculate the equivalent resistance of the external circuit, which consists of two resistors in parallel, using $R_{parallel} = \frac{R_1 R_2}{R_1 + R_2}$. $R_{parallel} = \frac{(6\,\Omega)(3\,\Omega)}{6\,\Omega + 3\,\Omega} = \frac{18\,\Omega^2}{9\,\Omega} = 2\,\Omega$.

3. Calculate the total resistance of the loop by adding the resistance of the connector $CD$ to the equivalent resistance of the external circuit: $R_{total} = r + R_{parallel}$. $R_{total} = 2\,\Omega + 2\,\Omega = 4\,\Omega$.

4. Calculate the induced current in the loop using Ohm's Law: $I = \frac{E}{R_{total}}$. $I = \frac{4\,V}{4\,\Omega} = 1\,A$.

5. Calculate the magnetic force on the conductor $CD$ using $F_m = IlB$. $F_m = (1\,A)(1.0\,m)(2\,T) = 2\,N$.

6. For constant velocity, the external force must balance the magnetic force, so $F_{ext} = F_m$. $F_{ext} = 2\,N$.