Question

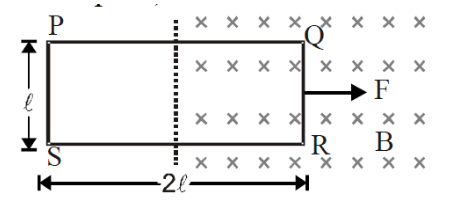
A rectangular loop PQRS, is being pulled with constant speed into a uniform transverse magnetic field by a force ${\text{F}}$ (as shown). E.M.F. induced in side PS and potential difference between points ${\text{P}}$ and ${\text{S}}$ respectively are (Resistance of the loop $= r)$

(A) Zero, $\dfrac{{{\text{Fr}}}}{{{\text{B}}\ell }}$
(B) Zero, zero
(C) Zero, $\dfrac{{{\text{Fr}}}}{{6\;{\text{B}}\ell }}$
(D) $\dfrac{{{\text{Fr}}}}{{6\;{\text{B}}\ell }},\dfrac{{{\text{Fr}}}}{{6\;{\text{B}}\ell }}$

Answer 1

The current flow can be generated by a changing magnetic field. To be more precise, a voltage will be produced if the magnetic flux through a coil is changed. This is known as EMF. The potential difference between any two points is defined as the amount of work carried out to move a unit charge from one point to another.

Formula Used: We will use the following formula to solve this question:
$F = B \times i \times \ell$
Where
${\text{F}}$ is force measured in newtons
$B$ is flux density
$i$ is current measured in amperes
$\ell$ is the length of the conductor in the magnetic field measured in metres.

Complete Step-by-Step Solution
According to the question, it is given to us that the rectangular loop PQRS is being pulled with a constant speed into a transverse magnetic field with force $F$ .
Also, we can observe that the side PS does not lie in the magnetic field. So, there will be no EMF induced over it. So, the EMF induced inside PS will be zero.
Since the loops are pulled under force $F$ at constant speed, because of the magnetic field, this force must balance the force on the current carrying wire.
Therefore, we will use
$F = B \times i \times \ell$
We can rewrite this formula as
$i = \dfrac{F}{{B\ell }}$
Now we will use the formula to find the potential difference between the points P and S.
${V_{PS}} = i{R_{PS}}$
Where
${V_{PS}}$ is the potential difference across P and S
And
${R_{PS}}$ is the resistance across points P and S
It is provided that the resistance across the loop whose perimeter is $6\ell$ is $r$ . So, the resistance across points P and S whose length is $\ell$ will be $\dfrac{r}{6}$ .
So, now we will substitute the value of $i$ and ${R_{PS}}$ in the above equation
Hence, we get
${V_{PS}} = \dfrac{F}{{B\ell }} \times \dfrac{r}{6} = \dfrac{{Fr}}{{6B\ell }}$
Hence, the correct option is (C).

Note
When the coil is completely inside the magnetic field, the coil's two ends become positive and the coil's other ends become negative. In each case, the coil's potential difference will be equal. Therefore, when two cells with equivalent electromotive force are connected to each other, no current flows through the coil, and there is no net electromotive force induced in the coil.