Question
Question: A rectangular loop of wire of size \(2.5cm\times 4cm\) carries a steady current of \(1A\). A straigh...
A rectangular loop of wire of size 2.5cm×4cm carries a steady current of 1A. A straight wire carrying 2A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i). the torque acting on the loop
(ii). Magnitude and direction of the force on the loop due to current carrying wire
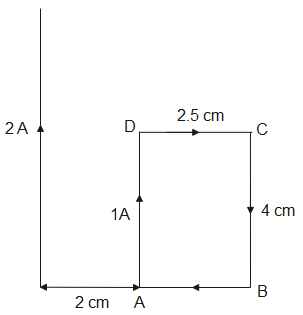
Solution
The torque acting on a current element is the cross product of magnetic dipole moment and magnetic field strength. Therefore, the torque acting on the element will be perpendicular to its plane. The force acting on a current carrying element is equal to the product of current and cross product of length and magnetic field and its direction depends on the direction of flow of current in both the elements.
Formulas used:
τ=M×B
F=I(l×B)
B=2πrμ0I
Complete answer:
The torque acting on the wire is given by the formula-
τ=M×B⇒τ=MBsinθ
Here, τ is the torque
M is the magnetic dipole vector
B is the magnetic field vector
θ is the angle between M and B
As the current in the loop is in the clockwise direction, the direction of magnetic dipole moment for the loop is in the paper. According to the right hand rule, the magnetic field vector is also into the plane of paper.
Therefore, the angle between magnetic field vector and magnetic dipole vector is 0.
Therefore, from the above equation,
τ=MBsin0⇒τ=0
Therefore, the torque which acts on the loop is zero.
(ii). The force acting on the loop due to the straight wire is given by-
F=I(l×B)
⇒F=IlBsinθ - (1)
Here, F is the force acting on the loop
I is the current in the straight wire
l is the length of the wire on which the force acts
B is the magnetic field vector due to which the force acts
θ is the angle between length vector and magnetic field vector
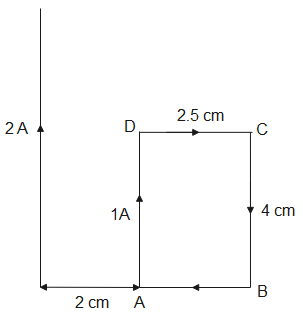
From the figure, the force acting on AB and DC are equal and opposite and hence cancel each other.
The magnetic field acting on the loop due to long straight wire is-
B=2πrμ0I - (2)
Here,
μ0 is the absolute permeability
I is the current in the straight wire
r is the distance from the straight wire
Substituting eq (1) in eq (2) for AD we get,
F=Il2πrμ0I
We substitute the given values in the above equation, we get,
F1=2πrμ0I2l⇒F1=2π×2μ0(2)2×4⇒F1=4π16μ0⇒F1=16×10−7N
The force acting on the arm AD is 16×10−7N and its direction is away from the long straight wire.
Similarly, the force acting on the arm BC is-
F2=IlB⇒F2=Il2πr′μ0I⇒F2=2πr′μ0I2l⇒F2=2π×(2+2.5)μ0(2)2×4⇒F2=2π×4.516μ0∴F2=7.11×10−7N
The force acting on the arm BC is 7.11×10−7N.
The total force acting on the loop due long straight wire is-
F=F1−F2⇒F=16×10−7N−7.1×10−7N⇒F=8.9×10−7N
Therefore, the total force acting on the wire is 8.9×10−7N and its direction is away from the straight long wire.
Note:
When current flows in the clockwise direction, the magnetic south pole is formed whereas when the current flows in the anticlockwise direction, the magnetic north pole is formed. According to the right hand rule, for a long straight wire, if the thumb represents the direction of flow of current then the fingers represent the direction of the magnetic field.
