Question

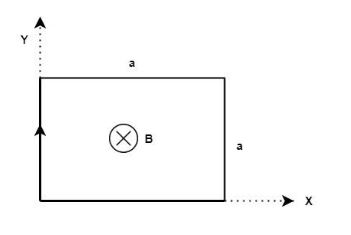
A rectangular loop of wire is oriented with the left corner at the origin, one edge along the x axis and the other edge along the y axis as shown in the figure. A magnetic field is into the page and has a magnitude that is given by $\beta = \alpha y$ where $\alpha$ is constant. Find the total magnetic force on the loop if it carries current i.

Answer 1

This is a particular case of moving charges in a magnetic field. We all know that moving charge means current. So, here the current is moving in a square loop with side “a” with magnetic field B in the inward direction and the value of the magnetic field is given by $\beta = \alpha y$. Apply the general formula for force of each side of a square loop and the sum to find the net force.

Formula used:
Here the formula for force is
$F = ilb\sin \theta$ ;
Where:
F = Force;
i = Current;
l = length;
b = magnetic force;
$\theta$ = Angle;

Complete step-by-step answer:
(Here the angle $\theta$ for each side of the loop is different)
The net force is equal to the sum of all the four forces:
${F_{Net}} = {F_1} + {F_2} + {F_3} + {F_4}$ ;
Put the integral formula in the above forces,
${F_{Net}} = i\int {(d{l_1} \times {B_1}) + i\int {(d{l_2} \times {B_2}) + i\int {(d{l_3} \times {B_3})} } } + i\int {(d{l_4} \times {B_4})}$ ;
Put the value in the above equation and solve;
Here, solve the vectors by the vector property:
($i \times j = k$ ;$j \times k = i$; $k \times i = j$) ; ( $j \times i = - k$; $k \times j = - i$; $i \times k = - j$);
Simplify the above equation further,
${F_{Net}} = \left[ {i\int_0^a {(\alpha y)} dy\left( { - \widehat i} \right)} \right] + ia\left( {a \times \alpha y\left( {\widehat j} \right)} \right) + i\int\limits_0^a {dy \times \left( {\alpha y} \right)\widehat i}$;
Solve, the integration by applying the integration property$\left( {\int {{a^n}} = \dfrac{{{a^{n + 1}}}}{{n + 1}}} \right)$ ,${F_{Net}} = - i\alpha \dfrac{{{a^2}}}{2}\widehat i + i\alpha {a^2}\widehat j + i\dfrac{{\alpha {a^2}}}{2}\widehat i$
The final value of ${F_{Net}}$is given as:
${F_{Net}} = i\alpha {a^2}\widehat j$;

Note: Go step by step apply the formula of force on each side and then solve the integration. Be careful in solving the integration and make sure to apply vector properties to solve equations involving vectors. Here the side AD is zero as the angle between the magnetic field and current is zero.