Question

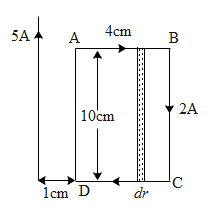
A rectangular loop of wire $4cm\times 10cm$ carries steady current of 2A. A straight long wire carrying 5A current is kept near the loop as shown. If the loop and the wire are coplanar, find the magnitude of the flux through the rectangular loop

Answer 1

In the above question it is given to us that there exists a wire 1 cm from the loop which carries current of 5A. Hence it will produce a magnetic field across the rectangular loop. Similarly the segments of the loop carry steady current as well. Hence each of the segments will also generate a magnetic field. Since the flux is given as the product of the area of the loop times the magnetic field, we will integrate the total flux across the rectangular area and determine the total magnetic flux.
Formula used:
$B=\dfrac{{{\mu }_{\circ }}i}{2\pi r}$
$d\phi =BA=Bldr$

Complete answer:

Let us say there is a straight current carrying wire carrying current equal to ‘i’. If we wish to calculate the magnetic field(B) at a distance r from the wire it is given by,
$B=\dfrac{{{\mu }_{\circ }}i}{2\pi r}$
Magnetic flux ($\phi$)is defined as the product of magnetic fields perpendicular to the plane of the given area times the magnitude of the area(A) mathematically written as $\phi =BA$. If we observe the above diagram, the wire carrying current of 5A is at a distance of 1cm from the rectangular loop. The magnetic field due to a wire varies as we move away from the wire. Let us say we wish to calculate a small amount of flux ($d\phi$)across the region (dA=ldr). Hence from the definition of flux we get the amount of flux equal to,
$\begin{aligned} & d\phi =BdA \\\ & \Rightarrow d\phi =\dfrac{{{\mu }_{\circ }}i}{2\pi r}ldr \\\ & \\\ \end{aligned}$
The above magnetic field varies with the distance. Hence we have to integrate the flux from segment AD to segment BC i.e. at a distance of 1cm to 4+1= 5cm we get. Hence the flux through the rectangular coil is,
$\begin{aligned} & \int{d\phi }=\int\limits_{1}^{5}{\dfrac{{{\mu }_{\circ }}i}{2\pi r}ldr} \\\ & \Rightarrow \phi =\dfrac{{{\mu }_{\circ }}il}{2\pi }\int\limits_{1}^{5}{\dfrac{dr}{r}}\text{, }\int{\dfrac{1}{x}}dx=\ln x \\\ & \Rightarrow \phi =\dfrac{{{\mu }_{\circ }}5\times 10\times {{10}^{-2}}}{2\pi }\left[ \operatorname{lnr} \right]_{1}^{5} \\\ & \Rightarrow \phi =\dfrac{25\times {{10}^{-2}}{{\mu }_{\circ }}}{\pi }\ln (5\times {{10}^{-2}}-1\times {{10}^{-2}})Wb \\\ & \Rightarrow \phi =\dfrac{25\times {{10}^{-2}}{{\mu }_{\circ }}}{\pi }\ln (5)Wb \\\ & \Rightarrow \phi =\dfrac{25\times {{10}^{-2}}\times 4\pi \times {{10}^{-7}}}{\pi }\ln (5)Wb \\\ & \Rightarrow \phi =100\times {{10}^{-9}}\ln (5)Wb=1.609\times {{10}^{-7}}Wb \\\ \end{aligned}$
Therefore the flux through the rectangular loop, due to wire which carries current of 5A is $1.609\times {{10}^{-7}}Wb$

Note:
The direction of the magnetic field is towards the plane of the paper. In order to determine the direction of magnetic field due to a current carrying wire, imagine that one wraps his right hand across the wire such that the thumb points to the direction of the current. Then the fingers curling the wire will indicate the direction of the magnetic field due to the wire.