Question
Question: A rectangular loop of side 10 cm and 3 cm moving out of a region of uniform magnetic field of 0.5 T ...
A rectangular loop of side 10 cm and 3 cm moving out of a region of uniform magnetic field of 0.5 T directed normal to the loop. If we want to move the loop with a constant velocity 1 cm/sec, then the required mechanical force is (Resistance of loop is 1milliohm)
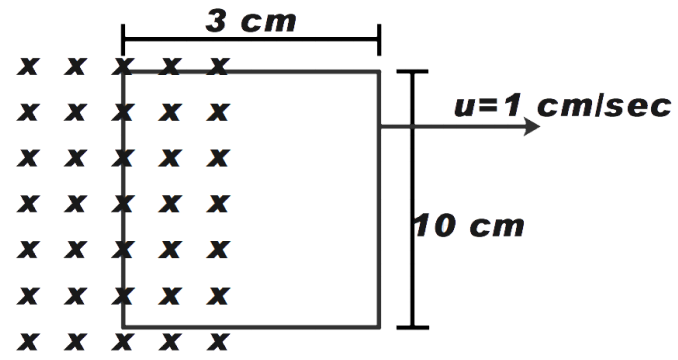
A. 2.25×10−3N
B. 4.5×10−3N
C. 9×10−3N
D. 1.25×10−3N
Solution
In this question we are asked to calculate the mechanical force. We know that force on a wire is given as the product of the magnetic field, length of the wire in the magnetic field and current. We will first calculate the value of current as other parameters such as magnetic field and length is known to us. Therefore, using these values we will calculate the force required.
Formula used:
V=dtdϕ
i=RV
F=ilB
Complete answer:
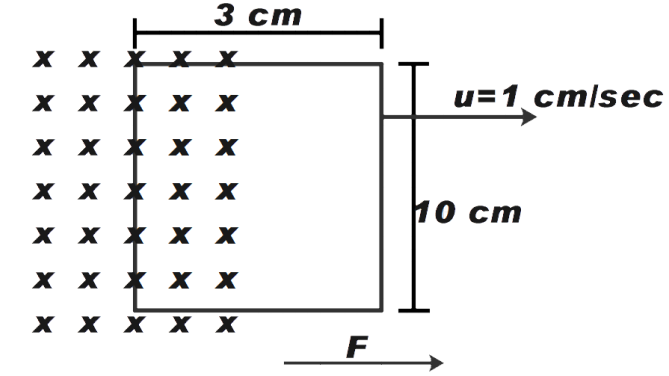
We asked to calculate the force required to move the loop with constant velocity of 1 cm/sec.
We know,
F=ilB
We have been given the length as 3 cm i.e. 0.03 m and resistance as 1 milli ohm which is 1×10−3Ω
Therefore, solving for current i,
We know that emf is given by,
V=dtdϕ …………….. (1)
Where, dϕ is the change in flux, which is given by
ϕ=BAcosθ …………. (2)
herecosθis taken as 1
After substituting (2) in equation (1)
We get,
V=dtd(0.5×0.03x) ……………. (since Area = 0.03x)
Therefore,
V=100015dtdx
We know, dtdx is the velocity of the loop
Therefore, after substituting
We get,
V=100015×1001
Therefore,
V=15×10−5 …………. (3)
Now, we know from Ohm’s law that,
i=RV
After substituting values
We get,
i=1×10−315×10−5
Therefore,
i=15×10−2
Now, substitute the value of i in equation (1)
We get,
F=15×10−2×3×10−2×0.5
Therefore,
F=2.25×10−3 N
So, the correct answer is “Option A”.
Note:
Magnetic field is a vector quantity that describes the magnetic influence on moving electric charges or electric current. A charge moving in a magnetic field experiences a force perpendicular to its own velocity and the magnetic field. Magnetic flux is defined as the number of magnetic field lines passing through a given closed surface area.
