Question

A rectangular hyperbola whose centre is $C$ is cut by any circle of radius $r$ in four points $P,Q,R$ And $S$ . Then if $C{P^2} + C{Q^2} + C{R^2} + C{S^2} = k{r^2}$ , find the value of $k$ .

Answer 1

Hint : In this question we need to find the value of $k$ . Therefore, here we will consider a circle and a hyperbola with a common centre. Then substitute the values of $x$ and $y$ from the equation of hyperbola into the equation of the circle, to determine the common point. Then , we will consider the equations as a quadratic equation in ${x^2}$ and ${y^2}$ and taking the common centre is $C\left( {0,0} \right)$ then, $P,Q,R,S$ be $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right),\left( {{x_4},{y_4}} \right)$ respectively. And, finally substituting the values and evaluating it we will get the required solution.

Complete step by step solution:

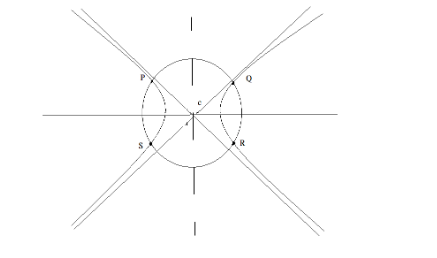
Now, we know that the equation of rectangular hyperbola is $xy = {c^2}$ .
And also, the equation of the circle is ${x^2} + {y^2} = {r^2}$ .
Let both the hyperbola and the circle have a common centre $C\left( {0,0} \right)$ .
From the equation of hyperbola, we have,
$y = \dfrac{{{c^2}}}{x}$ and $x = \dfrac{{{c^2}}}{y}$
Now, we need to find the common points of hyperbola and the circle.
So, let us substitute the value of $y$ from equation of hyperbola into the equation of circle, we get,
${x^2} + {\left( {\dfrac{{{c^2}}}{x}} \right)^2} = {r^2}$
${x^2} + \dfrac{{{c^4}}}{{{x^2}}} = {r^2}$
${\left( {{x^2}} \right)^2} - \left( {{r^2}} \right){x^2} + {c^4} = 0$
Let it be equation (1)
Now, let us take equation (1) as a quadratic equation in ${x^2}$ .
Thus, the sum of roots of the equation is,
${\left( {{x_1}} \right)^2} + {\left( {{x_2}} \right)^2} = {r^2}$ or ${\left( {{x_3}} \right)^2} + {\left( {{x_4}} \right)^2} = {r^2}$
Let it be equation (2)
Now, let us substitute the value of $x$ from equation of hyperbola into equation of circle, we get,
${y^2} + {\left( {\dfrac{{{c^2}}}{y}} \right)^2} = {r^2}$
${x^2} + \dfrac{{{c^4}}}{{{y^2}}} = {r^2}$
${\left( {{y^2}} \right)^2} - \left( {{r^2}} \right){y^2} + {c^4} = 0$
Let it be equation (3)
Now, let us take equation (3) as a quadratic equation in ${y^2}$ ,
Thus, the sum of roots of the equation is,
${\left( {{y_1}} \right)^2} + {\left( {{y_2}} \right)^2} = {r^2}$ or ${\left( {{y_3}} \right)^2} + {\left( {{y_4}} \right)^2} = {r^2}$
Let this be equation (4)
If the common centre is $C\left( {0,0} \right)$ then, $P,Q,R,S$ be $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right),\left( {{x_4},{y_4}} \right)$ respectively.
Hence, $C{P^2} = {x_1}^2 + {y_1}^2$
$C{Q^2} = {x_2}^2 + {y_2}^2$
$C{R^2} = {x_3}^2 + {y_3}^2$
$C{S^2} = {x_4}^2 + {y_4}^2$
Now, $C{P^2} + C{Q^2} + C{R^2} + C{S^2} = {x_1}^2 + {y_1}^2 + {x_2}^2 + {y_2}^2 + {x_3}^2 + {y_3}^2 + {x_4}^2 + {y_4}^2$
By rearranging the terms, we have,
$C{P^2} + C{Q^2} + C{R^2} + C{S^2} = {x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 + {y_1}^2 + {y_2}^2 + {y_3}^2 + {y_4}^2$
Let this be equation (5)
Substituting the values from equation (2) and equation (4) into equation (5), we get,
$\Rightarrow C{P^2} + C{Q^2} + C{R^2} + C{S^2} = {r^2} + {r^2} + {r^2} + {r^2} \\\ \Rightarrow C{P^2} + C{Q^2} + C{R^2} + C{S^2} = 4{r^2} \;$
Hence, comparing $C{P^2} + C{Q^2} + C{R^2} + C{S^2} = 4{r^2}$ with $C{P^2} + C{Q^2} + C{R^2} + C{S^2} = k{r^2}$ , we have,
$k = 4$
Hence, the value of $k$ is $4$ .
So, the correct answer is “4”.

Note : In this question it is important to note that the hyperbola whose asymptotes are at right angles at each other is called rectangular hyperbola. For a quadratic equation $a{x^2} + bx + c = 0$ , the sum of the roots of the equation is $\dfrac{{ - b}}{a}$ and the product of the roots of the equation is $\dfrac{c}{a}$ .