Question

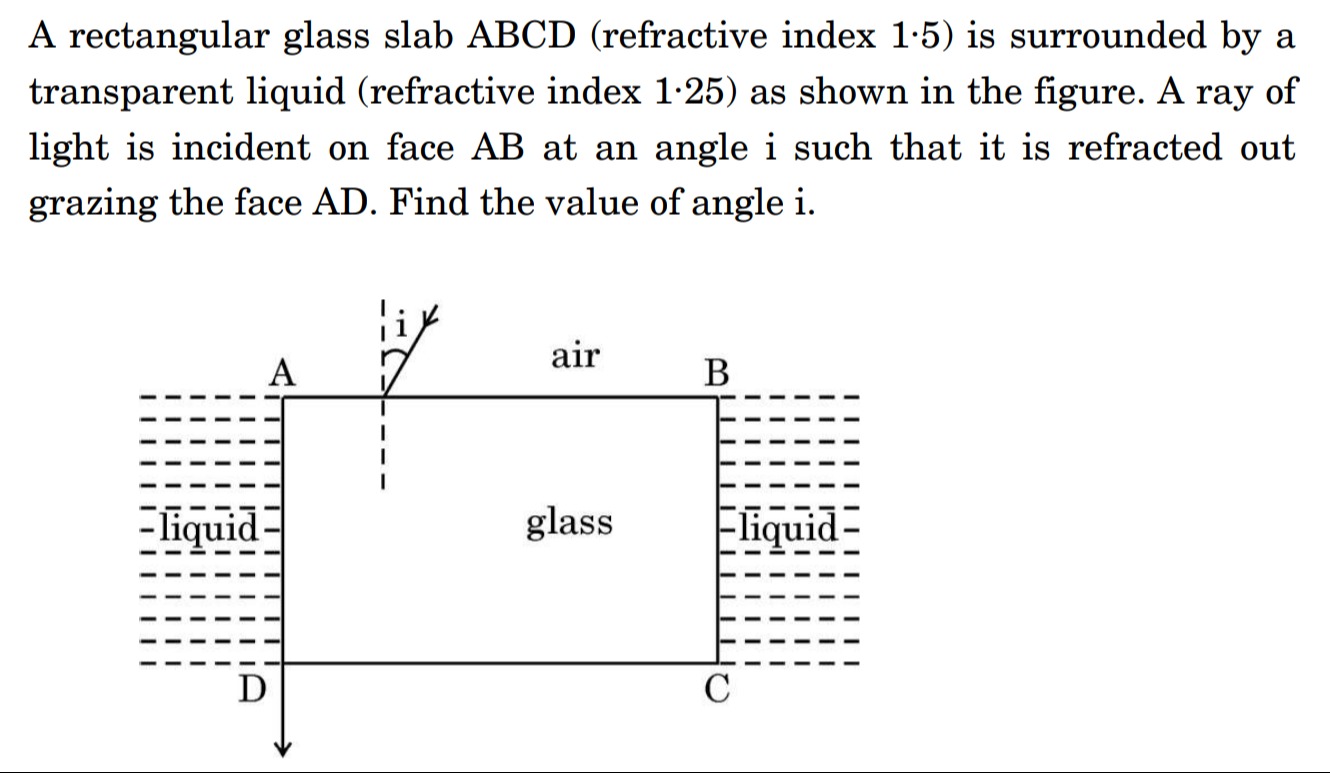
A rectangular glass slab ABCD (refractive index 1.5) is surrounded by a transparent liquid (refractive index 1.25) as shown in the figure. A ray of light is incident on face AB at an angle i such that it is refracted out grazing the face AD. Find the value of angle i.

Answer 1

arcsin(√11/4)

Answer 2

To find the value of angle $i$, we need to apply Snell's Law at two interfaces:

1. Air-Glass interface (face AB):
   Let $\mu_{air}$ be the refractive index of air, $\mu_{glass}$ be the refractive index of glass, $i$ be the angle of incidence in air, and $r_1$ be the angle of refraction in glass.
   Given: $\mu_{air} = 1$ (standard for air), $\mu_{glass} = 1.5$.
   According to Snell's Law:
   $\mu_{air} \sin(i) = \mu_{glass} \sin(r_1)$
   $1 \cdot \sin(i) = 1.5 \cdot \sin(r_1)$
   $\sin(i) = 1.5 \sin(r_1)$ (Equation 1)

2. Glass-Liquid interface (face AD):
   The ray travels inside the glass from face AB to face AD. Since the slab is rectangular, the normal to face AB is perpendicular to face AD. If the ray makes an angle $r_1$ with the normal to face AB inside the glass, then the angle of incidence ($r_2$) at face AD (with respect to the normal to AD) will be $90^\circ - r_1$.
   So, $r_2 = 90^\circ - r_1$.

   The problem states that the ray is refracted out grazing the face AD. This means the angle of refraction in the liquid ($r_3$) is $90^\circ$. This is the condition for grazing emergence (or critical angle condition).
   Let $\mu_{liquid}$ be the refractive index of the liquid.
   Given: $\mu_{liquid} = 1.25$.
   Applying Snell's Law at the glass-liquid interface:
   $\mu_{glass} \sin(r_2) = \mu_{liquid} \sin(r_3)$
   $1.5 \sin(r_2) = 1.25 \sin(90^\circ)$
   $1.5 \sin(r_2) = 1.25 \cdot 1$
   $\sin(r_2) = \frac{1.25}{1.5} = \frac{125}{150} = \frac{5}{6}$

3. Relate $r_1$ and $r_2$ and solve for $\sin(r_1)$:
   We know $r_2 = 90^\circ - r_1$.
   Therefore, $\sin(r_2) = \sin(90^\circ - r_1) = \cos(r_1)$.
   So, $\cos(r_1) = \frac{5}{6}$.

   Now, we find $\sin(r_1)$ using the identity $\sin^2(r_1) + \cos^2(r_1) = 1$:
   $\sin^2(r_1) = 1 - \cos^2(r_1)$
   $\sin^2(r_1) = 1 - \left(\frac{5}{6}\right)^2 = 1 - \frac{25}{36} = \frac{36 - 25}{36} = \frac{11}{36}$
   $\sin(r_1) = \sqrt{\frac{11}{36}} = \frac{\sqrt{11}}{6}$ (Since $r_1$ is an angle of refraction, it's acute and $\sin(r_1)$ is positive).

4. Find the value of angle $i$:
   Substitute the value of $\sin(r_1)$ back into Equation 1:
   $\sin(i) = 1.5 \sin(r_1)$
   $\sin(i) = 1.5 \cdot \frac{\sqrt{11}}{6}$
   $\sin(i) = \frac{3}{2} \cdot \frac{\sqrt{11}}{6}$
   $\sin(i) = \frac{\sqrt{11}}{4}$

   Therefore, the angle of incidence $i$ is:
   $i = \arcsin\left(\frac{\sqrt{11}}{4}\right)$