Solveeit Logo
Login

Question

Question: A rectangular glass slab ABCD of refractive index \({n_1},\) is immersed in water of refractive inde...

A rectangular glass slab ABCD of refractive index n1,{n_1}, is immersed in water of refractive index n2(n1>n2).{n_2}\left( {{n_1} > {n_2}} \right). A ray of light is incident at the surface AB of the slab as shown in the figure. The maximum value of angle of incidence αmax⁡{\alpha _{\max }}such that the ray comes out only from the other surface CD, is given by

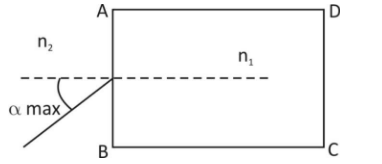
A. sin⁡−1[n1n2cos⁡(sin⁡−1n2n1)]{\sin ^{ - 1}}\left[ {\dfrac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]
B. sin⁡−1[n1cos⁡(sin⁡−11n2)]{\sin ^{ - 1}}\left[ {{n_1}\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{{{n_2}}}} \right)} \right]
C. sin⁡−1(n1n2){\sin ^{ - 1}}\left( {\dfrac{{{n_1}}}{{{n_2}}}} \right)
D. sin⁡−1(n2n1){\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)

Explanation

Solution

Concept of Total internal reflection is to be used. Then by shell’s law, the maximum value of α\alpha can be found.
Formula used:
1. Snell’s law
μ1  sin⁡  i  =μ2  sin⁡  r{\mu _1}\,\,\sin \,\,i\,\, = {\mu _2}\,\,\sin \,\,r
2. sin⁡  iC=μ2μ1\sin \,\,{i_C} = \dfrac{{{\mu _2}}}{{{\mu _1}}}
Where i is the angle of incidence
R is the angle of refraction
iC{i_C} is the critical angle
The ray travel from medium having refractive index μ1{\mu _1} to medium having refractive index μ2.{\mu _2}.

Complete step by step answer:
For the ray to emerge from the face CD, it has to undergo total interval reflection at face AD firstly as shown in the figure.

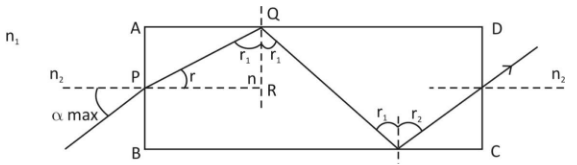
For total interval reflection to take place, angle of incidence, r1>{r_1} > critical angle iC.{i_C}.
i.e. r1>iC{r_1} > {i_C}
Now, sin⁡  r1=n2n1⇒r1=sin⁡−1(n2n1).......(1)\sin \,\,{r_1} = \dfrac{{{n_2}}}{{{n_1}}} \Rightarrow {r_1} = {\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right).......\left( 1 \right)
Now, let corresponding αmax⁡,{\alpha _{\max }}, r is the angle of redfraction
We know that,
r+r=90r + r = 90
⇒r=90−r,\Rightarrow r = 90 - r,
So, sin  r=sin⁡(90−r1)sin\,\,r = \sin \left( {90 - {r_1}} \right)
sin⁡  r=cos⁡r1   (as  cos⁡(90−θ)=sin⁡θ).......(2)\sin \,\,r = \cos {r_1}\,\,\,\left( {as\,\,\cos \left( {90 - \theta } \right) = \sin \theta } \right).......\left( 2 \right)
Now, we know that by Snell’s law the ratio of sin⁡r\sin r (angle of incidence) to sin⁡  i\sin \,\,i (angle of refraction) is constant and gives the refractive index in case of refraction.
So, for the face AB, by applying Snell’s law, we have
n2  sin⁡  αmax⁡=n1  sin⁡  r{n_2}\,\,\sin \,\,{\alpha _{\max }} = {n_1}\,\,\sin \,\,r
(as here angle of incidence =αmax⁡ = {\alpha _{\max }} and angle of refraction =r = r) and the ray is travelling from n2{n_2} to n1.{n_1}.
Putting equation (2) in it, we get n2  sin⁡  αmax⁡=n1  cos⁡  r1{n_2}\,\,\sin \,\,{\alpha _{\max }} = {n_1}\,\,\cos \,\,{r_1}
Putting r1{r_1} from equation (1) in it,
We have
n2  sin⁡  αmax⁡=n1  cos⁡ [sin⁡−1(n2n1)]{n_2}\,\,\sin \,\,{\alpha _{\max }} = {n_1}\,\,\cos \,\left[ {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]
⇒sin⁡  αmax⁡=n1n2  cos⁡ [sin⁡−1(n2n1)]\Rightarrow \sin \,\,{\alpha _{\max }} = \dfrac{{{n_1}}}{{{n_2}}}\,\,\cos \,\left[ {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]
⇒αmax⁡=sin⁡−1 [n1n2cos⁡(sin⁡−1)(n2n1)]\Rightarrow {\alpha _{\max }} = {\sin ^{ - 1}}\,\left[ {\dfrac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}} \right)\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]
Hence, option (A) is the correct option.

Note: r+r1=900r + {r_1} = {90^0}
This is because ΔPQR,\Delta PQR, is a right angled triangle so,
r+r1+900=1900r + {r_1} + {90^0} = {190^0} (by angle sum property)
r+r1=1900−900r + {r_1} = {190^0} - {90^0}
⇒r+r1=900\Rightarrow r + {r_1} = {90^0}.