Question
Question: A rectangular gate 3 m $\times$ 1 m stands vertical with water on one side of it hinged at the middl...
A rectangular gate 3 m × 1 m stands vertical with water on one side of it hinged at the middle. The force F required to the applied at the bottom to keep the gate in equilibrium is
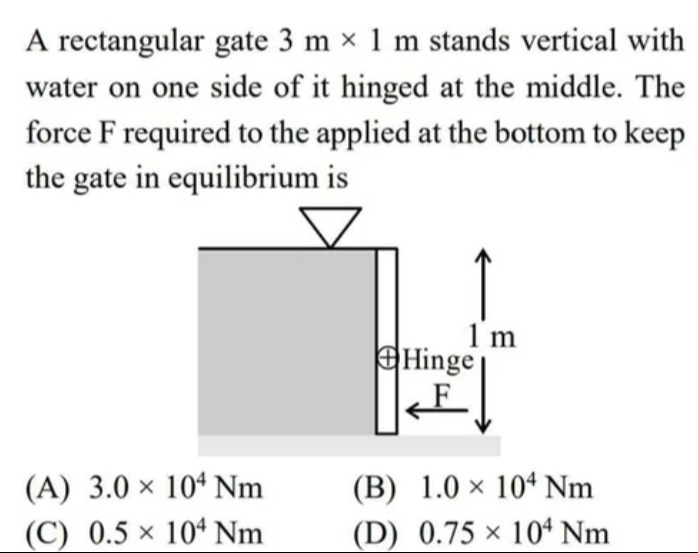
3.0 × 104 Nm
1.0 × 104 Nm
0.5 × 104 Nm
0.75 × 104 Nm
0.5 × 10^4 Nm
Solution
The dimensions of the rectangular gate are 3 m × 1 m. Let's assume the height is 3 m and the width is 1 m. The gate stands vertical with water on one side up to the top. The hinge is at the middle, i.e., at a height of 1.5 m from the bottom. The force F is applied at the bottom.
The hydrostatic force on the vertical gate is given by Fh=ρghˉA, where ρ is the density of water, g is the acceleration due to gravity, hˉ is the depth of the centroid of the gate from the free surface, and A is the area of the gate.
Here, height H=3 m, width W=1 m. Area A=H×W=3×1=3m2.
The centroid of the gate is at a height of 3/2=1.5 m from the bottom. Since the water level is at the top, the depth of the centroid from the free surface is hˉ=1.5 m.
Let's take ρ=1000kg/m3 and g=10m/s2.
Fh=1000×10×1.5×3=45000N=4.5×104N.
The hydrostatic force acts at the center of pressure. For a vertical rectangular plate with the top edge at the free surface, the center of pressure is at a depth of hcp=32H from the free surface.
So, hcp=32×3=2 m from the free surface (top).
The height of the center of pressure from the bottom is 3−2=1 m.
The hinge is at the middle of the gate, which is at a height of 1.5 m from the bottom.
The hydrostatic force Fh acts at a height of 1 m from the bottom.
The force F is applied at the bottom, at a height of 0 m from the bottom.
For equilibrium, the net torque about the hinge must be zero.
The torque due to the hydrostatic force about the hinge is τh=Fh×(1.5−1)=Fh×0.5. This torque tends to rotate the gate counter-clockwise (assuming water is on the left).
The torque due to the force F about the hinge is τF=F×(1.5−0)=F×1.5. The force F is applied horizontally to the left at the bottom, so it produces a clockwise torque.
For equilibrium, τh=τF.
Fh×0.5=F×1.5
4.5×104×0.5=F×1.5
2.25×104=1.5F
F=1.52.25×104=1.52.25×104=1.5×104N.
Let's assume the width is 3m and the height is 1m. The gate is vertical, so height is 1m. Hinged at the middle, so at 0.5m from the bottom. Water level at the top, so water depth is 1m.
Area A=1×3=3m2. Centroid depth from top hˉ=1/2=0.5 m.
Fh=ρghˉA=1000×10×0.5×3=15000N=1.5×104N.
Center of pressure depth from top hcp=32H=32×1=32 m.
Height of center of pressure from bottom = 1−32=31 m.
Hinge is at 0.5 m from the bottom. Force F is at 0 m from the bottom.
Torque due to Fh about hinge = Fh×(0.5−1/3)=Fh×(3/6−2/6)=Fh×(1/6).
Torque due to F about hinge = F×(0.5−0)=F×0.5.
For equilibrium, Fh×(1/6)=F×0.5.
1.5×104×(1/6)=F×0.5.
0.25×104=0.5F.
F=0.50.25×104=0.5×104N.
