Question
Question: A rectangular conductor LMNO placed in a uniform magnetic field of 0.5T. The field is directed perpe...
A rectangular conductor LMNO placed in a uniform magnetic field of 0.5T. The field is directed perpendicular to the plane the conductor. When the arm MN of length of 20 cm is moved towards the left with a velocity of 10 ms−1, calculate the emf induced in the arm. Given the resistance of the arm to be 5Ω(assuming that other arms and of negligible resistance) find the value of the current in the arm.
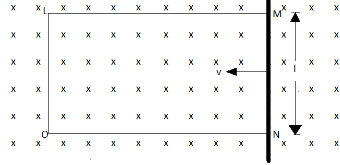
Solution
To find out the induced emf on a conductor, the component of magnetic field(B) which is perpendicular to length (l) and velocity (v) is taken into account. Induced emf is given as e=−dtdϕ. Where, ϕ=B.A. Then applying ohm's law we find the current in this arm I=Re, where R is the resistance of the arm.
Complete step by step answer:
Given the magnetic field B=0.5T. The length of the rod, l=20cm=0.2m and its velocity, v=10m/s. We know that according to Faraday's law the induced EMF is negative of the rate of change of flux. e=−dtdϕ.Where, ϕ is the flux =B.A
The negative sign is neglected as it shows the direction which is opposite to the direction of change of flux.
e=dxd(BA)
As the magnetic field B is constant and area ( A) is equal to the product of length (l) and breadth(b) of the rod, we get the induced EMF as
e=Bdtd(lb)
⇒e=Bldtdb
We know that it is the velocity of the rod v=dtdb.
Substituting the value, we get e=Blv.
So,e=0.5×0.2×10=1V
To find the current in this arm we use ohm's law, I=Re
Substituting the value of potential difference e and resistance R we get,
I=51 ∴I=0.2A
Hence, the value of current is 0.2 A.
Note: We should know that the electromotive force induced in a current carrying wire of length ‘l’, moving with a velocity of ‘v’ in a magnetic field of intensity ‘B’ is given as e=Blv. Also, emf is induced only when one of the three conditions are fulfilled: The magnetic field changes, or the area of the conductor changes or the angle between the external field and the area vector changes continuously. If emf is induced then there will always be flow of electric current and the same can be found easily using Ohm's law if the resistance of the conductor is known.
