Solveeit Logo
Login

Question

Question: A rectangular conducting loop of width 20 cm and infinite length, mass m = 10 gm and net resistance ...

A rectangular conducting loop of width 20 cm and infinite length, mass m = 10 gm and net resistance 20 Ω\Omega is dropped into a uniform magnetic field B = 2T such that field is normal to the plane of loop. The terminal velocity attained by the loop is (g = 10 m/s2^2)

Answer

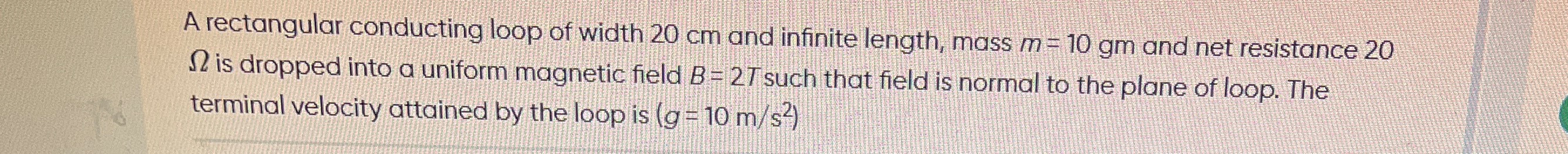
12.5 m/s

Explanation

Solution

Explanation of the solution:

  1. Forces acting on the loop: As the rectangular loop falls, it experiences a downward gravitational force (Fg=mgF_g = mg) and an upward magnetic force (FmF_m) due to the induced current.

  2. Motional EMF: When the loop falls with velocity vv, the electromotive force (EMF) induced across its width ll (the part cutting the magnetic field lines) is given by:

    E=Blv\mathcal{E} = Blv

  3. Induced Current: The induced current II in the loop is determined by Ohm's law:

    I=ER=BlvRI = \frac{\mathcal{E}}{R} = \frac{Blv}{R}

    where RR is the net resistance of the loop.

  4. Magnetic Force: The upward magnetic force on the current-carrying segment of length ll in the magnetic field BB is:

    Fm=IlBF_m = IlB

    Substituting the expression for II:

    Fm=(BlvR)lB=B2l2vRF_m = \left(\frac{Blv}{R}\right) l B = \frac{B^2 l^2 v}{R}

    According to Lenz's law, this force opposes the motion, hence it acts upwards.

  5. Terminal Velocity Condition: Terminal velocity (vtv_t) is achieved when the net force on the loop becomes zero. This occurs when the upward magnetic force balances the downward gravitational force:

    Fm=FgF_m = F_g B2l2vtR=mg\frac{B^2 l^2 v_t}{R} = mg

  6. Solving for Terminal Velocity (vtv_t):

    vt=mgRB2l2v_t = \frac{mgR}{B^2 l^2}

  7. Substitute the given values: Given:

    • Mass, m=10 gm=0.01 kgm = 10 \text{ gm} = 0.01 \text{ kg}
    • Acceleration due to gravity, g=10 m/s2g = 10 \text{ m/s}^2
    • Net resistance, R=20 ΩR = 20 \, \Omega
    • Magnetic field, B=2 TB = 2 \text{ T}
    • Width of the loop, l=20 cm=0.2 ml = 20 \text{ cm} = 0.2 \text{ m}
    vt=(0.01 kg)(10 m/s2)(20 Ω)(2 T)2(0.2 m)2v_t = \frac{(0.01 \text{ kg})(10 \text{ m/s}^2)(20 \, \Omega)}{(2 \text{ T})^2 (0.2 \text{ m})^2} vt=0.1×204×0.04v_t = \frac{0.1 \times 20}{4 \times 0.04} vt=20.16v_t = \frac{2}{0.16} vt=20016v_t = \frac{200}{16} vt=12.5 m/sv_t = 12.5 \text{ m/s}

The terminal velocity attained by the loop is 12.5 m/s.