Question

A rectangular conducting loop of length $4\sqrt 2 m$ and breadth $4m$ carrying a current of $5A$ in the anti-clockwise direction is placed in the $xy$-plane. The magnitude of the magnetic induction field vector B at the intersection of the diagonal is: $({\text{Use }}{u_0} = 4\pi \times {10^{ - 7}}N{A^{ - 2}})$

A) $1.2 \times {10^{ - 6}}T$
B) $1.2 \times {10^{ - 5}}T$
C) $2.4 \times {10^{ - 6}}T$
D) $2.4 \times {10^{ - 5}}T$
E) $1.2 \times {10^{ - 7}}T$

Answer 1

We can consider the sides of the rectangle as independent finite wires and then sum up the magnetic induction field vector for each wire to get the final magnetic induction field vector B of the rectangle.

Formula used:
$B = \dfrac{{{\mu _0}Idl\sin \theta }}{{4\pi {r^2}}}$
Where B is the magnetic field of a finite wire,
${\mu _0}$ is the permeability of free space,
$I$ is the current flowing in the wire,
$\theta$ is the angle between $\mathop {dl}\limits^ \to$ and $\hat r$
The direction of the $\mathop B\limits^ \to$ can be figured out by using the right-hand rule. Here since the current is flowing in the opposite direction, therefore the direction of $\mathop B\limits^ \to$ is emerging out of the plane.

Complete step by step solution:
Magnetic induction is the production of an electromotive force across an electrical conductor in a changing magnetic field. It is also known as electromagnetic induction. According to Faraday’s law, for a closed circuit, the induced electromotive force is equal to the rate of change of the magnetic flux enclosed by the circuit.

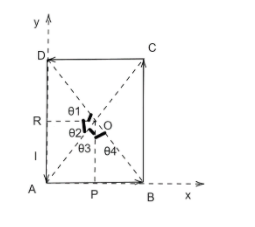
We will mark the angles ${\theta _1},{\theta _2},{\theta _3},{\theta _4}$, as such:
Points $R$ and $P$ are the mid-points of side $AD$ and $AB$.

Since the given current $I = 5A$
The length of $AD = 4\sqrt 2 m$
And the length of $AB = 4m$
For wire of finite length according to the Biot-Savart Rule, magnetic induction field:
$\Rightarrow B = \dfrac{{{\mu _0}I(\sin {\theta _1} + \sin {\theta _2})}}{{4\pi d}}......eq(1)$
For the wire $AB$:
$\Rightarrow \sin {\theta _3} = \dfrac{{AP}}{{OP}} = \dfrac{2}{{\sqrt {4 + 8} }} = 0.577$
$\Rightarrow \sin {\theta _4} = \dfrac{{PB}}{{OP}} = \dfrac{2}{{\sqrt {4 + 8} }} = 0.577$
$\Rightarrow d = \dfrac{{AD}}{2} = \dfrac{{4\sqrt 2 }}{2} = 2\sqrt 2$
$\Rightarrow {B_{AB}} = {B_{CD}} = \dfrac{{{\mu _0} \times 5}}{{4\pi \times 2\sqrt 2 }}(0.577 + 0.577)$
$\Rightarrow \dfrac{{{{10}^{ - 7}} \times 5}}{{2\sqrt 2 }} \times 2 \times 0.577 = 2.04 \times {10^{ - 7}}T$
For the wire $AD$
$\Rightarrow \sin {\theta _1} = \dfrac{{RD}}{{DO}} = \dfrac{{2\sqrt 2 }}{{\sqrt {4 + 8} }} = 0.816$
$\Rightarrow \sin {\theta _2} = \dfrac{{RA}}{{OA}} = \dfrac{{2\sqrt 2 }}{{\sqrt {4 + 8} }} = 0.816$
$\Rightarrow d = RO = 2m$
$\Rightarrow {B_{AD}} = {B_{BC}} = \dfrac{{{\mu _0} \times 5}}{{4\pi \times 2}}(0.816 + 0.816)$
$\Rightarrow \dfrac{{{{10}^{ - 7}} \times 5}}{2} \times 2 \times 0.816 = 4.08 \times {10^{ - 7}}$
Therefore, the total magnetic induction field:
$\Rightarrow {B_{total}} = {B_1} + {B_2} + {B_3} + {B_4}$
$\Rightarrow (2 \times 2.04 \times {10^{ - 7}}) + (2 \times 4.08 \times {10^{ - 7}}) = 1.2 \times {10^{ - 6}}T$

The correct answer is (A), $1.2 \times {10^{ - 6}}T$.

Note: The magnetic field due to a finite wire must not be confused with the magnetic field from an infinite wire. The magnetic field due to an infinite wire is $\dfrac{{{\mu _0}I}}{{2\pi r}}$, where ${\mu _0}$ is the permeability of free space, $I$ is the current flowing in the wire, and $r$ is the distance of the wire from the point from where the magnetic field is to be calculated.