Solveeit Logo
Login

Question

Question: A rectangular coil of wire of \(500\) turns having an area \(10\times 5c{{m}^{2}}\)carries a current...

A rectangular coil of wire of 500500 turns having an area 10×5cm210\times 5c{{m}^{2}}carries a current of 2A2A in a magnetic field of induction 2×10−3T2\times {{10}^{-3}}T. Let us assume that the plane of the coil is parallel to the field. Then what will be the torque on the coil (in NmNm)?
A.0.1 B.0.01 C.0.001 D.1 \begin{aligned} & A.0.1 \\\ & B.0.01 \\\ & C.0.001 \\\ & D.1 \\\ \end{aligned}

Explanation

Solution

The torque on the rectangular coil because of the presence of magnetic field can be found by taking the product of the number of turns, current flowing through the coil, area of the coil and the magnetic field and the sine of the angle. The area vector will be always perpendicular to the plane and it has been mentioned that the plane is parallel to field. This will help you in answering this question.

Complete answer:

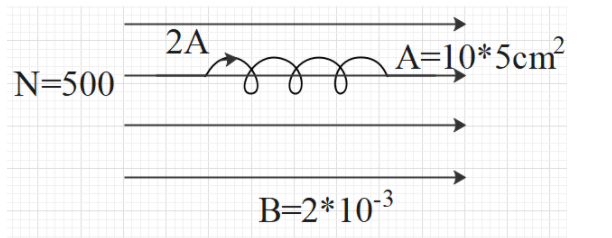
The torque on the rectangular coil because of the presence of magnetic field can be found by taking the product of the number of turns, current flowing through the coil, area of the coil and the magnetic field and the sine of the angle. This can be written as,
τ=NIABsin⁡θ\tau =NIAB\sin \theta
It has been already mentioned in the question that the number of turns in the rectangular coil of wire will be,
N=500N=500
The current flowing can be written as,
I=2AI=2A
Area of the coil can be mentioned as,
A=(10×5)×10−4m2A=\left( 10\times 5 \right)\times {{10}^{-4}}{{m}^{2}}
The magnetic field can be shown as,
B=2×10−3TB=2\times {{10}^{-3}}T
The angle between the area and the magnetic field vector can be written as θ\theta .
As we know, the area vector will be always perpendicular to the plane and it has been mentioned that the plane is parallel to field, therefore the angle between area and field will be,
θ=90∘\theta =90{}^\circ
Substituting the values in this equation can be written as,
τ=(500×2×(10×5)×10−4×2×10−3)sin⁡90∘ τ=0.01Nm \begin{aligned} & \tau =\left( 500\times 2\times \left( 10\times 5 \right)\times {{10}^{-4}}\times 2\times {{10}^{-3}} \right)\sin 90{}^\circ \\\ & \tau =0.01Nm \\\ \end{aligned}
Hence the value of the torque has been calculated.

This has been mentioned as option B.

Note:
Torque is defined as the amount of the force that can result in the rotation of a body about an axis. Force is the quantity that results in the acceleration of a body in linear kinematics.in the same way, torque is the quantity resulting in angular acceleration. Thus torque is considered as the rotational equivalent of the force.