Solveeit Logo
Login

Question

Question: A rectangular coil having \(60\) turns and area of \(0.4{{m}^{2}}\) is held at right angles to a uni...

A rectangular coil having 6060 turns and area of 0.4m20.4{{m}^{2}} is held at right angles to a uniform magnetic field of flux density 5×10−5T5\times {{10}^{-5}}T . What is the magnetic flux passing through it?

Explanation

Solution

We know that the area vector of a material will be normal to the surface of the coil. Here the coil is placed perpendicular to the magnetic field. Therefore the area vector will be parallel to the magnetic field. This may help you to solve this question.

Formula used:
The equation for the magnetic flux is given as,
ϕ=NBAcos⁡θ\phi =NBA\cos \theta
Where NNbe the number of turns of the rectangular coil, BB be the magnetic flux density over there, AA be the area of cross section of the coil and θ\theta be the angle between the area vector of the coil and the magnetic field.

Complete answer:
First of all let us consider the values mentioned in the question.

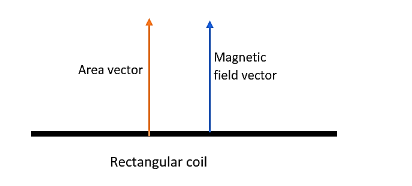
The number of turns of the given rectangular coil is given as,
N=60N=60
Area of cross section is mentioned as,
A=0.4m2A=0.4{{m}^{2}}
Magnetic field in the region is given as,
B=5×10−5TB=5\times {{10}^{-5}}T
It is also mentioned that the field is uniform.
The equation for the magnetic flux can be written as,
ϕ=NBAcos⁡θ\phi =NBA\cos \theta
Here θ\theta be the angle made between the area vector of the coil and the magnetic field present there.
As we all know the area vector of a material is perpendicular to the surface of material. Here the field and the coil are placed in perpendicular directions. Therefore we can say that the area vector will be parallel to the magnetic field vector.

That is,
θ=0∘\theta =0{}^\circ
Let us substitute all these values in the equation.
ϕ=60×5×10−5×0.4cos⁡0 ϕ=1.2×10−3Wb \begin{aligned} & \phi =60\times 5\times {{10}^{-5}}\times 0.4\cos 0 \\\ & \phi =1.2\times {{10}^{-3}}Wb \\\ \end{aligned}

Note:
The measure of magnetic flux is the direct result of the material that is forming a magnet. Where the magnetic flux density is given as the product of the magnetic flux and the area of cross section where the flux is present. This is the difference between magnetic flux and magnetic flux density.