Solveeit Logo
Login

Question

Question: A rectangular coil (dimensions \(5cm \times 2.5cm\)) with 100 turns, carrying a current 3A in the cl...

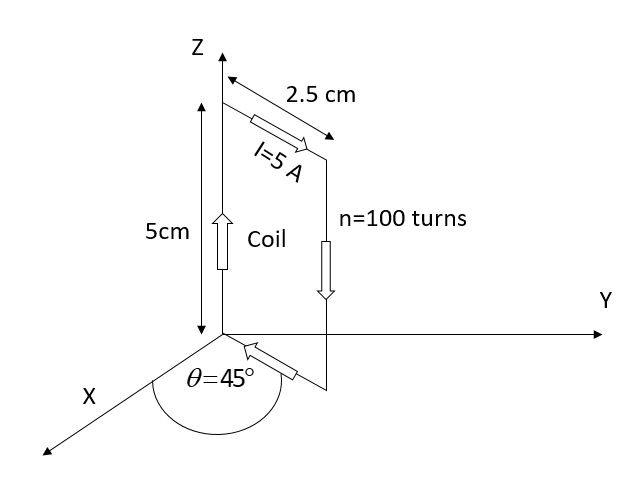
A rectangular coil (dimensions 5cm×2.5cm5cm \times 2.5cm) with 100 turns, carrying a current 3A in the clockwise directions kept centered at the origin and in the X-Z plane. A magnetic field of 1T1T is applied along the X-axis. If the coil is titled through 45∘45^\circ about Z-axis, then the torque of the coil is:
A 0.55Nm0.55Nm
B. 0.27Nm0.27Nm
C. 0.38Nm0.38Nm
D. 0.42Nm0.42Nm

Explanation

Solution

Here torque on current-carrying rectangular loop placed in a uniform magnetic field. The current flowing in the loop is in a clockwise direction. The direction is given by using the right-hand screw rule. The magnetic field is proportional to the current and the number of turns in the coil.

Complete step by step answer:
According to question here we have N (no. of turns) = 100turns, I (current) =3A, B (magnetic field) = 1T
And θ\theta (angle) =45∘45^\circ
Area of the rectangular loop (A) =5cm×2.5cm=12.5cm−2 = 5cm \times 2.5cm = 12.5 c{m^{ - 2}}

We know torque(τ⃗)(\vec \tau ) =∣M⃗×B⃗∣ = \left| {{\rm{\vec M}} \times {\rm{\vec B}}} \right|
Where M is the magnetic moment and B is the magnetic field.
⇒τ⃗=I(A⃗×B⃗)\Rightarrow \vec \tau = {\rm{I(\vec A}} \times {\rm{\vec B)}} (Where A is the area of cross-section)
If the loop has N turns, then the net torque acting on the loop
τ=NIABsinθ\tau = {\rm{NIABsin}}\theta
⇒τ=100×3×12.5×sin45∘\Rightarrow \tau = 100 \times 3 \times 12.5 \times {\rm{sin45}}^\circ
⇒τ=0.27Nm\Rightarrow \tau = 0.27Nm

The torque of the coil is 0.27Nm. Hence, option (B) is correct.

Additional information:
If the current-carrying loop is aligned in such a way that the plane of the loop is parallel to the direction of the magnetic field, so the torque acting on the loop τ=NIAB\tau = {\rm{NIAB}}
If the current-carrying loop aligned in such way that the plane of the loop is perpendicular in the direction of the magnetic field then τ=0\tau = 0

Note:
The maximum torque acts on the loop or coil. The magnetic field which is parallel to the plane of the loop is called the radial magnetic field. When torque acting on the coil is zero, the loop in the position of equilibrium. Thus torque acting in a uniform magnetic field may or may not zero.