Question

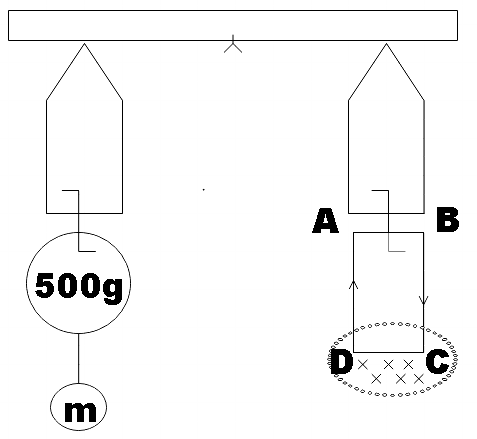
A rectangular coil ABCD is hung from one side of a balance as shown in the figure. A 500g mass is added to the other arm to balance the weight of the coil. A current of 9.8A is passed through the coil and a constant magnetic field of 0.4T acting inward (in XZ plane) is switched on such that only an arm CD of length 1.5cm lies in the field. The additional mass m must be added to regain the balance is

A. 4g
B. 5g
C. 6g
D.7g

Answer 1

As a first step, you could consider the case when neither current nor the magnetic field is present and then balance the forces. Then, you could go for the next case when both are present. On balancing the forces that are acting on both arms and then rearranging and then substituting accordingly will give the required mass.
Formula used:
Magnetic force,
$F=BIL\sin \theta$

Complete answer:
In the question, we are given a rectangular coil ABCD hung from the arm that is balanced by a 500g mass on the arm. Therefore, we could say that,
${{W}_{ABCD}}=Mg=500\times g=500\times 9.8$
Where, M is the mass of the coil.
Now, we are told that 9.8A current is then passed through the coil and the arm CD of the coil lies in a 0.4T magnetic field. Then, quite obviously this arm CD will experience a magnetic force and in order to balance this force a mass m is added to the other arm. We are supposed to find m.
Magnetic force is given by,
$F=BIL\sin \theta$
Where, $\theta$ is the angle between L and B which here is $90{}^\circ$
Substituting the values we get,
$F=0.4\times 9.8\times 1.5$
This force will be equal to the weight of the new body introduced on the other arm of the balance. So,
$mg=0.4\times 9.8\times 1.5$
$\Rightarrow m=\dfrac{0.4\times 9.8\times 1.5}{9.8}$
$\therefore m=6g$
Therefore, we found the mass to be equal to 6g.

Hence, option C is found to be the correct answer.

Note:
We are basically balancing the forces acting on the two arms. For the final part we haven’t considered the weight of the coil and weight of the 500g body. This is because we already know that they are equal in magnitude and they balance each other. So, we have directly considered the weight of the m massed body balancing the magnetic force.