Question

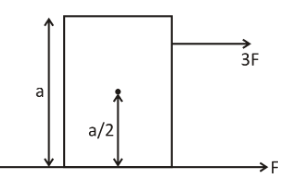
A rectangular block of mass $M$ and height $a$ is resting on a smooth level surface. A force F is applied to one corner as shown in the figure. At what point should a parallel force $3F$ be applied in order that the block shall undergo pure translational motion? Assume normal contact force between the block and the surface passes through the centre of gravity of the block.

A. $\dfrac{a}{3}$ vertically above the centre of gravity
B. $\dfrac{a}{6}$ vertically above the centre of gravity
C. No such point exists
D. It is not possible

Answer 1

A body undergoes pure translational motion, if it does not have any curvilinear motion. Curvilinear motion is due to the presence of torque about a certain point. If torque becomes zero, then the body undergoes pure translational motion.

Formula used:
The formula which defines torque about a certain point is as follows:
$\tau = F \times r$ …… (1)
Where,
$\tau$ indicates torque.
$F$ indicates the magnitude of the force.
$r$ indicates the distance between the point about which the body is rotating and the applied force.

Complete step by step answer:
In the given question, we are supplied the following data:
There is a rectangular block whose mass is $M$ and height $a$ .The block is resting on a smooth level surface.A force F is applied to one corner.A parallel force $3F$ is also applied and we are asked to find the point of application of this force, if the body needs have pure translational motion.

To begin with, we will need to draw the free body diagram of the rectangular block, in order to have the better understanding of the situation as described in the question. The free body diagram of the block is given below:

Let the distance at which the force $3F$ is applied, from the centre of gravity of the block, be $x$ . So, if the body needs to move forward in a pure translational motion, then the net torque acting at that point must be equal to zero. Since, there are two forces, we can write the expression for the net torque as:
$3F \times x - F \times \dfrac{a}{2} = 0 \\\ \Rightarrow 3F \times x = F \times \dfrac{a}{2} \\\ \Rightarrow 3x = \dfrac{a}{2} \\\ \therefore x = \dfrac{a}{6}$
Hence, the force must be applied at a height of $\dfrac{a}{6}$ vertically above the centre of gravity.

The correct option is B.

Note: While solving this problem, most of the students don’t really think about the torque. It is the torque, which is associated with a rotating body, under the application of opposite forces. A body undergoing a curvilinear motion can’t have torque equal to zero. A body can’t be rotated if the two equal forces are applied in the same direction.