Solveeit Logo
Login

Question

Question: A rectangle with sides \[2m - 1\] and \[2n - 1\] is divided into square of unit length by drawing pa...

A rectangle with sides 2m−12m - 1 and 2n−12n - 1 is divided into square of unit length by drawing parallel lines as shown in diagram, then the number of rectangle possible with odd side length is

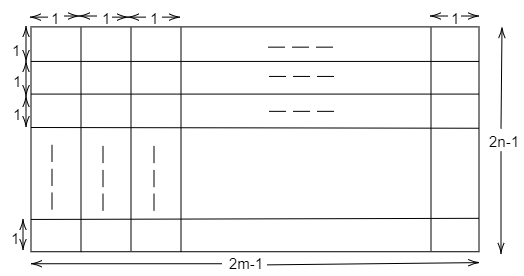
(A) (m+n−1)2{\left( {m + n - 1} \right)^2}
(B) 4m+n−1{4^{m + n - 1}}
(C) m2n2{m^2}{n^2}
(D) m(m+1)n(n+1)m(m + 1)n(n + 1)

Explanation

Solution

There will be 2m2m vertical lines and 2n2n horizontal lines. To form a rectangle, we need two lines from each set. But the sides need to be odd numbered, so we will select one odd and one even numbered side from both sets. And then using the concept of permutation we will find the number of rectangles possible with odd side length.

Complete step by step solution:
Here, a rectangle with sides 2m−12m - 1 and 2n−12n - 1 is divided into squares of unit length by drawing parallel lines.
So, to divide a rectangle with sides 2m−12m - 1 and 2n−12n - 1 is divided into squares of unit length by drawing parallel lines we need 2m2m vertical lines and 2n2n horizontal lines.
Also, to form a rectangle we must select two horizontal lines and two vertical lines.
Here, we require possible rectangles with odd side length, for this we have to select one odd and one even numbered side from both the sets of 2m2m vertical lines and 2n2n horizontal lines.
From 2m2m vertical lines, mm will be odd numbered sides and other half mm will be even numbered sides and from 2n2n horizontal lines, nn will be odd numbered sides and other half nn will be even numbered sides.
As we know that, nCr=n!r!(n−r)!^n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}} where nn is the number of items and rr is the number of items being chosen at a time.
Number of ways of selecting one vertical odd numbered side == mC1^m{C_1}
=m!1!(m−1)!= \dfrac{{m!}}{{1!(m - 1)!}}
On simplification, we get
Number of ways of selecting one vertical odd numbered side =m(m−1)!1!(m−1)! = \dfrac{{m\left( {m - 1} \right)!}}{{1!(m - 1)!}}
=m= m
Similarly,
Number of ways of selecting one vertical even numbered side == mC1^m{C_1}
=m= m
Number of ways of selecting one horizontal odd numbered side == nC1^n{C_1}
=n= n
Number of ways of selecting one horizontal even numbered side == nC1^n{C_1}
=n= n
Total number of rectangle possible with odd side length =m×m×n×n = m \times m \times n \times n
=m2n2= {m^2}{n^2}
Therefore, the number of rectangles possible with odd side length is m2n2{m^2}{n^2}.
Hence, option (C) is correct.

Note: We can also solve this problem by another method.
We have, number of ways of selecting vertical sides =1+3+5+....+(2m−1) = 1 + 3 + 5 + .... + (2m - 1) which is equal to m2{m^2}.
Similarly, the number of ways of selecting horizontal sides =1+3+5+....+(2n−1) = 1 + 3 + 5 + .... + (2n - 1) which is equal to n2{n^2}.
So, the number of rectangles possible with odd side length == number of ways of selecting vertical sides ×\times number of ways of selecting horizontal sides.
Therefore, we get the number of rectangles possible with odd side length =m2n2 = {m^2}{n^2}.
Hence, option (C) is correct.