Question

A rectangle is to have an area of 16 square inches. How do you find its dimensions so that the distance from one corner to the midpoint of a nonadjacent side is a minimum?

Answer 1

To solve the above question, we should know about the rectangle. A rectangle is a 2D shape in geometry, having 4 sides and 4 corners. Its two sides meet at right angles. It has 4 angles, each measuring 90 degrees. The sides of a rectangle have the same lengths and are parallel. The area of the rectangle is $\left( length\times breadth \right)$ and the perimeter of the rectangle is $2\left( length+breadth \right)$.

Complete step-by-step solution:
We have given that the area of the rectangle is $16{{m}^{2}}$.
We can write is also as:
$\begin{aligned} & \Rightarrow Area=\left( length\times breadth \right) \\\ & \Rightarrow 16=length\times breadth \\\ \end{aligned}$
Now by using question we will draw a diagram of the line cutting through the rectangle and use the Pythagorean Theorem which is as:
${{\left( Hypotenuse \right)}^{2}}={{\left( length \right)}^{2}}\times {{\left( breadth \right)}^{2}}$
Let $l$ be the length of the rectangle and $w$ be the breadth of the rectangle

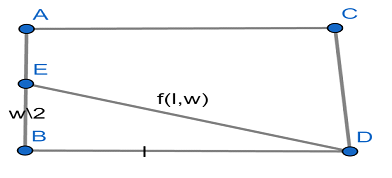
Now we will find the length of hypotenuse say $f\left( l,w \right)$, we get
$\Rightarrow f\left( l,w \right)=\sqrt{{{l}^{2}}+{{\left( \dfrac{w}{2} \right)}^{2}}}$
Now by using the area equation $16=length\times breadth$we will make $f\left( l,w \right)$ into single variable
$\begin{aligned} & \Rightarrow 16=\left( length\times breadth \right) \\\ & \Rightarrow l=\dfrac{16}{w} \\\ \end{aligned}$
Now substitute $l$ by $\dfrac{16}{w}$ in $f\left( l,w \right)=\sqrt{{{l}^{2}}+{{\left( \dfrac{w}{2} \right)}^{2}}}$, we get
$\begin{aligned} & \Rightarrow f\left( l,w \right)=\sqrt{{{l}^{2}}+{{\left( \dfrac{w}{2} \right)}^{2}}} \\\ & \Rightarrow f\left( w \right)=\sqrt{{{\left( \dfrac{16}{w} \right)}^{2}}+{{\left( \dfrac{w}{2} \right)}^{2}}} \\\ \end{aligned}$
Now solving the above equation we get

& \Rightarrow f\left( w \right)=\sqrt{\dfrac{256}{{{w}^{2}}}+\dfrac{{{w}^{2}}}{4}} \\\ & \Rightarrow f\left( w \right)=\sqrt{\dfrac{1024+{{w}^{4}}}{4{{w}^{2}}}} \\\ & \Rightarrow f\left( w \right)=\dfrac{\sqrt{{{w}^{4}}+1024}}{2w} \\\ \end{aligned}$$ So by the above equation the value $w$ exists between $0< w< \infty $. Since we have to find the minimum value of $w$ so for this find the derivative of $f\left( w \right)$.$$\Rightarrow f\left( w \right)=\dfrac{\sqrt{{{w}^{4}}+1024}}{2w}$$ Now by using quotient rule $\dfrac{d\left( u.v \right)}{dx}=\dfrac{v\dfrac{du}{dx}-u\dfrac{dv}{dx}}{{{v}^{2}}}$ on above equation we get $$\begin{aligned} & \Rightarrow f\grave{\ }\left( w \right)=\dfrac{\dfrac{4{{w}^{3}}\left( 2w \right)}{2\left( \sqrt{{{w}^{4}}+1024} \right)}-2\sqrt{{{w}^{4}}+1024}}{4{{w}^{2}}} \\\ & \Rightarrow f\grave{\ }\left( w \right)=\dfrac{\dfrac{4{{w}^{4}}}{\sqrt{{{w}^{4}}+1024}}-\dfrac{2\left( {{w}^{4}}+1024 \right)}{\sqrt{{{w}^{4}}+1024}}}{4{{w}^{2}}} \\\ & \Rightarrow f\grave{\ }\left( w \right)=\dfrac{2{{w}^{4}}-2048}{4{{w}^{2}}\sqrt{{{w}^{2}}+1024}} \\\ \end{aligned}$$ Now by more simplifying, we get $$\Rightarrow f\grave{\ }\left( w \right)=\dfrac{{{w}^{4}}-1024}{2{{w}^{2}}\sqrt{{{w}^{4}}+1024}}$$ Now set the above equation equals to zero, we get $\begin{aligned} & \Rightarrow \dfrac{{{w}^{4}}-1024}{2{{w}^{2}}\sqrt{{{w}^{4}}+1024}}=0 \\\ & \Rightarrow {{w}^{4}}-1024=0 \\\ & \\\ \end{aligned}$ Now add $1024$ on both sides, we get $\begin{aligned} & \Rightarrow {{w}^{4}}=1024 \\\ & \Rightarrow w=\sqrt[4]{1024} \\\ & \Rightarrow w=4\sqrt{2} \\\ \end{aligned}$ Therefore the derivative of $f\left( w \right)$ does not exist when $w=0$. Now we have to find the extrema, first find the function values for the endpoints of the domain, $0$ and $\infty $, and for the critical value, $4\sqrt{2}$ . Since $0$ and $\infty $cannot putted into $f\left( w \right)$ **Therefore, $w=4\sqrt{2}$ is the only critical point on the interval $\left( 0,\infty \right)$, and it is relatively minimum and it is the smallest breadth value that fits the parameter.** **Note:** We can go wrong by creating the Pythagorean formula, here I created by using$\dfrac{w}{2}$ and $l$, which means that$w=4\sqrt{2}$ is the side being bisected. Also make sure the quotient rule $\dfrac{d\left( u.v \right)}{dx}=\dfrac{v\dfrac{du}{dx}-u\dfrac{dv}{dx}}{{{v}^{2}}}$ which we used is also correct.