Question
Question: A reaction proceeds through two paths I and II to convert \[X \to Z\]. What is the correct relations...
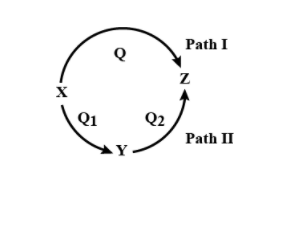
A reaction proceeds through two paths I and II to convert X→Z. What is the correct relationship between, Q, Q1, and Q2 (Q represents a change in internal energy, here)?
A. Q=Q1×Q2
B. Q=Q1+Q2
C. Q=Q2−Q1
D. Q=Q2Q1
Solution
We know that the Internal energy is a state function. In the question above, Q is the change in internal energy. We all know that,
δQ=δU+δW.
Complete step by step answer:
We can define Internal Energy as the energy that is random and disordered motion of the molecule. To make it clear, we should know that the change in internal energy for a reaction is always the same whether it occurs in one step or the reaction either occurs in two steps or is in multiple steps that is in a series of steps. So in the above reaction, if X is converted to Z in single step, then the internal energy that is Q released and when the change happens through two step that is X to and then Y to Z, then the internal energy release while change from X to Y that is Q1 and the internal energy released from change while Y to Z that is Q will definitely be equal to the energy while direct conversion of X to Z. so Q1 that is released while conversion of X to Y and Q2 that is released while conversion from Y to Z will be equal to Q that is released from conversion of X to Z.
Internal energy (Q) is a state function.
⇒QXZ=QXY+QYZ
⇒Q=Q1+Q2
Therefore, the correct answer is option (B).
Note: The internal energies released in a multi-step reaction will be equal to when the reaction happens in just one step. The enthalpy of reaction is defined as the internal energy of the system.
