Question

A ray travelling along the line $3x - 4y = 5$ after being reflected from a line $l$ travels along the line $5x + 12y = 13$. Then the equation of the line is:
A) $x + 8y = 0$
B) $x = 8y$
C) $32x + 4y = 65$
D) $32x - 4y + 65 = 0$

Answer 1

Let the equation of $l$ be $y = mx + c$. Now, from the incident ray and reflected ray equation, we can find the point of intersection which satisfies the line $l$. And we know that if ${a_1}x + {b_1}y + {c_1} = 0$ and ${a_2}x + {b_2}y + {c_2} = 0$ are two lines given, then the angle bisector is given by
$\dfrac{{{a_1}x + {b_1}y + {c_1}}}{{\sqrt {{a_1}^2 + {b_1}^2} }} = \pm \dfrac{{{a_2}x + {b_2}y + {c_2}}}{{\sqrt {{a_2}^2 + {b_2}^2} }}$

Complete step-by-step answer:
So here, a ray is travelling along the line $3x - 4y = 5$ and after being reflected from a line $l$ travels along the line $5x + 12y = 13$.
Here the line $l$ has equation $y = mx + c$.

Here, let $AB$ is the incident ray. That means $AB$ has the equation $3x - 4y = 5$. Similarly, $BC$ is the reflected ray with the equation $5x + 12y = 13$. So here, $B$ is the common point of intersection of all three lines.
Let $\left( {{x_1},{y_1}} \right)$ be the coordinates of $B$.
So, let's solve both the incident and reflected rays.
$3x - 4y = 5$ (1)
$5x + 12y = 13$ (2)
Now, multiplying $5$ with equation (1) and $3$ with equation (2), then subtracting, equation (2) from (1), we get
$5\left( {3x - 4y} \right) - 3\left( {5x + 12y} \right) = 5 \times 5 - 3 \times 13 \\\ \- 56y = - 14 \\\ y = \dfrac{{ - 14}}{{ - 56}} \\\ y = \dfrac{1}{4} \\\$
So, from equation (1), $3x - 4y = 5$
$3x = 5 + 4y \\\ x = \dfrac{{5 + 4y}}{3} = \dfrac{{5 + 4 \times \dfrac{1}{4}}}{3} = \dfrac{{5 + 1}}{3} \\\ x = 2 \\\$
So, $\left( {{x_1},{y_1}} \right) = \left( {2,\dfrac{1}{4}} \right)$ are the coordinates of $B$.
Now, $B$ also lies in line $l$
Here line $l$: $y = mx + c$
So, it will be
$\dfrac{1}{4} = 2m + c$
Now we know that the angle of incidence is equal to the angle of reflection.

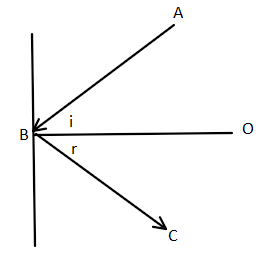
So, here, $\angle ABO$ represents angle of incidence $i$. And $\angle OBC$ represents angle of reflection $r$. So,
$i = r \\\ \angle ABO = \angle OBC \\\$
Thus we can say that $OB$ is the angle bisector of two lines $AB$ and $BC$. Thus, for any two lines ${a_1}x + {b_1}y + {c_1} = 0$ and ${a_2}x + {b_2}y + {c_2} = 0$, equation of angle bisector is
$\dfrac{{{a_1}x + {b_1}y + {c_1}}}{{\sqrt {{a_1}^2 + {b_1}^2} }} = \pm \dfrac{{{a_2}x + {b_2}y + {c_2}}}{{\sqrt {{a_2}^2 + {b_2}^2} }}$
Now, here equation of $OB$, we get
$\dfrac{{3x - 4y - 5}}{{\sqrt {{3^2} + {4^2}} }} = \pm \dfrac{{\left( {5x + 12y - 13} \right)}}{{\sqrt {{5^2} + {{12}^2}} }} \\\ \dfrac{{3x - 4y - 5}}{5} = \pm \dfrac{{\left( {5x + 12y - 13} \right)}}{{13}} \\\$
Here two cases are possible.
Case one: If we take positive value,
$\dfrac{{3x - 4y - 5}}{5} = + \dfrac{{\left( {5x + 12y - 13} \right)}}{{13}} \\\ 39x - 52y - 65 = 25x + 60y - 65 \\\ 14x = 112y \\\ x = \dfrac{{112}}{{14}}y \\\ x = 8y{\text{ (3)}} \\\$
Or $y = \dfrac{1}{8}x$
Case two: If we take negative value
$\dfrac{{3x - 4y - 5}}{5} = - \dfrac{{\left( {5x + 12y - 13} \right)}}{{13}} \\\ 39x - 52y - 65 = - 25x - 60y + 65 \\\ 64x + 8y - 130 = 0 \\\ 32x + 4y - 65 = 0{\text{ (4)}} \\\$
So, we got two equations of $OB$.
Also, we know that line $l$ and $OB$ are perpendicular.
So, ${m_1}{m_2} = - 1$
So, for case one,
${m_l} = m \\\ {m_{OB}} = \dfrac{1}{8} \\\ {m_l}.{m_{OB}} = - 1 \\\ m.\dfrac{1}{8} = - 1 \\\ m = - 8 \\\$
For case two,
${m_l} = m \\\ {m_{OB}} = - 8 \\\ m.\left( { - 8} \right) = - 1 \\\ m = \dfrac{1}{8} \\\$
And also, we had got
$\dfrac{1}{4} = 2m + c$
So, for case one: $m = - 8$
$\dfrac{1}{4} = 2\left( { - 8} \right) + c \\\ c = \dfrac{1}{4} + 16 \\\ c = \dfrac{{65}}{4} \\\$
So, equation of line $l$ becomes $y = mx + c$
$y = - 8x + \dfrac{{65}}{4} \\\ \Rightarrow 4y + 32x = 65 \\\$
For case two: $m = \dfrac{1}{8}$
$\dfrac{1}{4} = 2m + c \Rightarrow \dfrac{1}{4} = \dfrac{2}{8} + c \\\ c = 0 \\\$
So, equation of line $l$ becomes $y = mx + c$
$y = \dfrac{1}{8}x \\\ x = 8y \\\$

So, the correct answers are “Option B” and “Option C”.

Note: When any ray gets reflected, then the angle between incident and reflected ray are bisected by normal at their point of intersection. And also, we know that the angle between two lines with slope ${m_1}{\text{ and }}{m_2}$is given by $\tan \theta = \dfrac{{|{m_1} - {m_2}|}}{{|1 + {m_1}{m_2}|}}$.