Solveeit Logo
Login

Question

Question: A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and...

A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ=AR. If the angle of prism A=60∘A = {60^ \circ }and refractive index of material of prism is 3.\sqrt 3 .Calculate angle θ\theta

Explanation

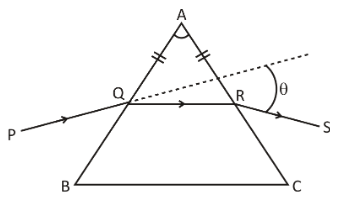
Solution

Apply law of refraction to find the angle of refraction after first refraction and then use properties of the isosceles triangle and laws of refraction on the surface AC to find the angle of emergence and then use the formula of angle of deviation to find angle θ\theta .

Complete step by step answer:
Let angle of incidence for ray PQ is ∠i\angle i and angle of refraction is ∠r1\angle {r_1}
Using snell’s law we have,
sin⁡∠isin⁡∠r1=μ=3\dfrac{{\sin \angle i}}{{\sin \angle {r_1}}} = \mu = \sqrt 3
Also
∠AQR=90∘−∠r1\angle AQR = {90^ \circ } - \angle {r_1}
And ∠AQR=∠ARQ\angle AQR = \angle ARQ( sides corresponding to the equal angle in isosceles triangle are equal)
And ∠AQR+∠ARQ+∠A=180∘\angle AQR + \angle ARQ + \angle A = {180^ \circ }(as sum of all angles of a triangle is 180)
⇒∠ARQ=180−602=60∘\Rightarrow \angle ARQ = \dfrac{{180 - 60}}{2} = {60^ \circ }
⇒∠r1=90−60=30∘\Rightarrow \angle {r_1} = 90 - 60 = {30^ \circ }
Putting value of ∠r1\angle {r_1} we have,
sin⁡∠isin⁡30∘=3\dfrac{{\sin \angle i}}{{\sin {{30}^ \circ }}} = \sqrt 3
⇒sin⁡∠i=3sin⁡30∘ ⇒sin⁡∠i=32\Rightarrow \sin \angle i = \sqrt 3 \sin {30^ \circ }\\\ \Rightarrow \sin \angle i= \dfrac{{\sqrt 3 }}{2}
⇒∠i=60∘\Rightarrow \angle i = {60^ \circ }

Now we will find the angle of deviation on the first surface AB. As angle of incidence is 60 degrees and angle of refraction is 30 degrees, if we take the difference of these two angles we will get an angle of deviation. So angle of deviation on surface AB,
δ1=∠i−∠r1 ⇒δ1=60∘−30∘ ⇒δ1=30∘{\delta _1} = \angle i - \angle {r_1} \\\ \Rightarrow{\delta _1}= {60^ \circ } - {30^ \circ } \\\ \Rightarrow{\delta _1}= {30^ \circ }
Now, as AQ=AR it means rays will be symmetric about the perpendicular bisector of ΔAQR\Delta AQR from A.
So deviation in the second surface (surface AC) will be same.
Therefore,
Deviation in surface AC δ2=δ1=30∘{\delta _2} = {\delta _1} = {30^ \circ }
So total deviation will be sum of these two deviations
Hence, total deviation θ=δ1+δ2 ⇒θ=30∘+30∘ ∴θ=60∘\theta = {\delta _1} + {\delta _2} \\\ \Rightarrow\theta = {30^ \circ } + {30^ \circ } \\\ \therefore\theta = {60^ \circ }

Therefore, correct answer is θ=60∘\theta = {60^ \circ }.

Note: Here in the surface AB when angle of incidence is 60∘{60^ \circ } then angle of refraction is 30∘{30^ \circ } as AQ is equal to AR it means angle of incidence in surface AC will be same as angle of refraction in surface AB therefore for surface AC angle of refraction will be 60 if you add the deviations in the surfaces you will get the value of theta.