Question
Question: A ray OP of monochromatic light is incident on the face AB of prism ABCD near vertex B at an inciden...
A ray OP of monochromatic light is incident on the face AB of prism ABCD near vertex B at an incident angle of 60∘ (see figure). If the refractive index of the material of the prism is 3, which of the following is (are) correct?
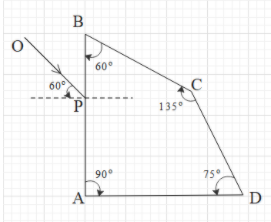
Solution
Use the Snell’s law and find the angle of refraction at face AB. Then find the angle of incidence at face CD. Calculate the critical angle for these mediums and check whether the ray reflects internally.
Formula used:
μisini=μrsinr
θc=sin−1(μ1)
Complete answer:
In this solution, we will use Snell's law for refraction of light at the interface of two mediums when the light ray passes from one medium into another medium.
i.e. μisini=μrsinr ….. (i),
where i and r are the angle of incidence and angle of refraction at the interface. μi is the refractive index of the medium from which the ray incidents and μr is the refractive index of the medium into which the ray passes after refraction.
First, the light ray enters from air into the glass prism from face AB. The ray is incident on AB at angle of incidence of 60∘. Therefore, for this case, i=60∘, μi=1 and μr=3. Let the angle of refraction at this face be r1.
Substitute the values in equation (i).
⇒1.sin60∘=3sinr1
⇒23=3sinr1
⇒sinr1=21
⇒r1=sin−1(21)=30∘.
Let us assume that the refracted ray falls on the face CD.

From the figure, we get the angle of incidence at face CD is 45∘.
Now, the light ray is passing through glass (denser medium) and it will be entering the air (rarer medium) after refraction.
When a light rays travelling in a denser medium hits the interface of the denser and a rarer medium, it may refract and pass into the rarer medium or may reflect internally.
The condition for total internal reflection of the light ray is that the angle of incidence at the interface must be more than the critical angle. The critical angle for the interface of air and a denser medium is given as θc=sin−1(μ1), where μ is the refractive index of the denser medium.
Therefore, the critical angle in the given case is θc=sin−1(31)=35.26∘.
Now we know that the angle of incidence at CD is more than the critical angle. Therefore, the ray will undergo total internal reflection.
Therefore, option A is correct.
After reflecting at CD, the ray will fall on the face AD.
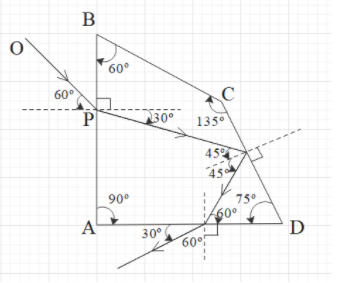
From the figure, we get the angle of incidence at AD is 30∘.
Since the angle of incidence at AD is less than the critical angle, the ray will come out from AD.
Therefore, option B is correct.
This means that i=30∘, μi=3 and μr=1. Let the angle of refraction at this face be r2.
Substitute the values in equation (i).
⇒3.sin30∘=1.sinr2
⇒23=sinr2
⇒r2=sin−123=60∘.
The first incident ray at AB makes an angle of 60∘ with the horizontal and the emergent at D is making an angle of 30∘ as shown.
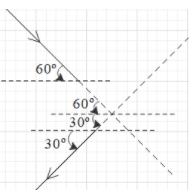
Therefore, the angle between the incident ray and the emergent ray is 90∘.
This means that the option C is correct.
Hence, the correct options are A, B and C.
Note:
Even if we do not know about the critical angle, we can still figure out whether the light ray will pass into the rarer medium or it will reflect into the same medium.
For this, assume that the ray passes into the other medium and apply Snell’s law. If the light ray really passes into the rarer medium, we will get a possible value of the angle of refraction. If not, then we will not have any possible value for the angle of refraction.
