Question

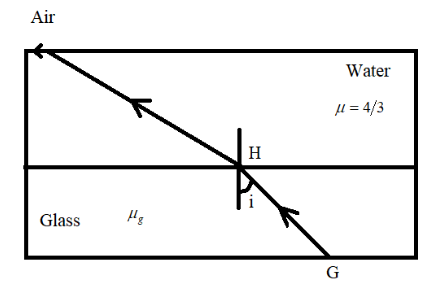
A ray of light travels in the fashion as shown in the figure. After passing through water the ray grazes along the water-air interface the value of refractive index of ${\mu _g}$ in terms of $i$ given refractive index of water is:
A. $\dfrac{1}{{\sin i}}$
B. $\dfrac{1}{{4\sin i}}$
C. $\dfrac{4}{{3\sin i}}$
D. None of these

Answer 1

The phenomenon of refraction of light occurs when light travels through two differing mediums with different refractive indices. The concept of refraction and the laws of refraction are applied in accordance with Snell's law to determine the relation between the refractive index of glass. Separate equations relating the glass-water medium and the water-air medium are constructed and equated to find the required answer.

Complete step by step answer:
The above problem revolves around the concept of the phenomenon of refraction through different mediums. When a light ray travels from one medium to another, that is, when the ray of light from one medium falls on the second medium, then a part of the light is said to be refracted inside the second medium with a change in its direction or path.

Refraction is defined as the phenomenon wherein there is a change in the path of light or more specifically the bending of the light rays due to the difference in the medium it is travelling in. Refraction of light occurs due to its differing speeds in both the mediums, that is, the speed of light changes causing a change in path.Here, there is a combination of media which is taken into consideration and as we can see the light is incident from a glass surface onto the surface of water and undergoes refraction and then again suffers a change in its path when travelling from water to air.

As per the laws of refraction, it is said that when a ray which travels from an optically denser medium to an optically rarer medium it tends to suffer a change in its direction and it tends to bend away from the normal. As we can see in the given diagram, the ray bends away from the normal and hence the refractive index of glass will be more than that of water. The angle which the light ray makes with the normal when it strikes the surface of another medium is called the angle of incidence which is given to be $i$ and the ray $GH$ is said to be the path of the incident ray. The angle it makes after refraction is called the angle of refraction denoted by $r$.

Since the light travels in a combination of media we will take each pair of media separately and determine equations for each of them. Let us first consider the glass-water medium. The refractive index is given by law known as the Snell’s law for refraction which is given by the equation:
${}^1{\mu _2} = \dfrac{{\sin i}}{{\sin r}}$
Here, ${}^1{\mu _2}$ represents the refractive index of the first medium with respect to the second medium. We consider the first medium to be glass and the second medium to be water. Here, since the glass-water medium is considered and since the refraction takes place from the denser medium to the rarer medium the above equation for Snell’s law becomes:
${}^g{\mu _w} = \dfrac{{\sin r}}{{\sin i}}$

The refractive index of one medium with respect to another is given by the ratio of refractive indices of the two mediums and hence the above equation becomes:
$\dfrac{{{\mu _g}}}{{{\mu _w}}} = \dfrac{{\sin r}}{{\sin i}}$
By cross multiplying the terms we get:
${\mu _g}\sin i = {\mu _w}\sin r$
We now an equation for the refractive index of the glass medium by rearranging the terms:
${\mu _g} = \dfrac{{{\mu _w}\sin r}}{{\sin i}}$
We are already given the refractive index of water which is given to be ${\mu _w} = \dfrac{4}{3}$. Hence we get:
${\mu _g} = \dfrac{{4\sin r}}{{3\sin i}}$ ---------($1$)

Now it can be seen that the angle of refraction $r$will be equivalent to the angle of incident of the light when travelling from water to air medium. This is because of the alternate angles law which states that alternate angles that are made are equal. Let the angle of incidence of light from water to air be given by $i'$. Hence we can see that $\angle r = \angle i'$ as illustrated in the diagram below:

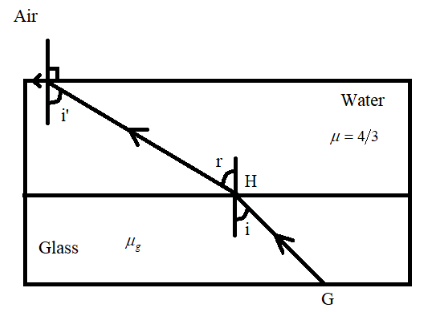
Hence by using this relation we can construct another equation for the refractive index of the water-air medium. It can be observed that the total internal reflection is taking place and hence the refracted ray is parallel to the medium thus making the value of angle of refraction equal to ${90^ \circ }$.

We apply the same Snell’s law equation here and even in this case light is travelling from a denser medium to a rarer one since water has a greater refractive index compared to air. Hence we get the equation:
${}^w{\mu _a} = \dfrac{{\sin r'}}{{\sin i'}}$
Here, we consider the first medium to be water and the second medium to be air. Since, the refractive index of one medium with respect to another is given by the ratio of refractive indices of the two mediums and hence the above equation becomes:
$\dfrac{{{\mu _w}}}{{{\mu _a}}} = \dfrac{{\sin r'}}{{\sin i'}}$
By cross multiplying the terms we get:
${\mu _w}\sin i' = {\mu _a}\sin r'$
Here, since the angle of incidence that is $i'$ is said to be equal to $r$we get:
${\mu _w}\sin r = {\mu _a}\sin r'$

We now make $\sin r$the subject to determine its value:
$\sin r = \dfrac{{{\mu _a}\sin r'}}{{{\mu _w}}}$
Since the value of $r' = {90^ \circ }$ and the refractive indices of water and air are $\dfrac{4}{3}$ and $1$ respectively we substitute these values in the above equation to get:
$\sin r = \dfrac{{1 \times \sin {{90}^ \circ }}}{{\dfrac{4}{3}}}$
Since, $\sin {90^ \circ } = 1$ we get:
$\sin r = \dfrac{1}{{\dfrac{4}{3}}}$
$\Rightarrow \sin r = \dfrac{3}{4}$
Hence we substitute this value in equation ($1$) to get:
${\mu _g} = \dfrac{{4 \times \dfrac{3}{4}}}{{3\sin i}}$
By further solving the equation we get:
$\Rightarrow {\mu _g} = \dfrac{4}{3} \times \dfrac{3}{4} \times \dfrac{1}{{\sin i}}$
The common terms get cancelled out and we get:
${\mu _g} = \dfrac{1}{{\sin i}}$
Thus this is the relationship between the refractive index of glass and the angle of incidence.
Hence, the relation between ${\mu _g}$ and $i$ is given by ${\mu _g} = \dfrac{1}{{\sin i}}$.

Therefore, the correct answer is option A.

Note: The common error which can be made in problems of this kind is that a single refractive index value is found which is wrong. The refractive index is always determined with respect to another medium and here since there is a combination of media through which light is travelling in the refractive index with respect to another medium is considered (ratio of refractive indices). Another common misconception is that since the refractive index of glass is usually $1.5$, this value may be considered and substituted which is incorrect.