Question

A ray of light travels from an optically denser to rarer medium. The critical angle for the two media is C. The maximum possible deviation of the ray will be
${\text{A}}{\text{. }}\dfrac{\pi }{2} - C \\\ {\text{B}}{\text{. }}2C \\\ {\text{C}}{\text{. }}\pi - 2C \\\ {\text{D}}{\text{. }}\pi - C \\\$

Answer 1

First, we need to draw ray diagrams for a ray of light travelling from denser to rarer medium considering critical angle and total internal reflection. The maximum deviation will occur in case of total internal reflection when angle of incidence is greater than the critical angle.

Complete step by step answer:
The critical angle of a medium can be defined as the angle of incidence of a light ray in the denser medium which is such that the angle of refraction obtained is equal to 90$^\circ$. This can be represented as shown in the figure.

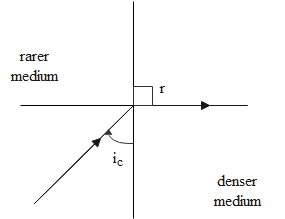
Now consider a general case where we have light ray travelling from a denser medium to a rarer medium at an angle of incidence i and let r be the angle of refraction. The deviation produced in the angle of the light when it passes from the denser medium to rarer medium is equal to difference between the angle of refraction and the angle of incidence. Let the deviation be $\delta$ then it is given as
$\delta = r - i$

Now if $i = C$ (the critical angle) then $r = \dfrac{\pi }{2}$. In this case, the deviation is given as
$\delta = \dfrac{\pi }{2} - C$
The maximum deviation in the light ray will occur when the light will go internal reflection. In case of reflection, the angle of incidence is equal to the angle of reflection.

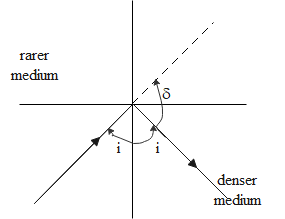
In this case, the deviation produced is given as
$\delta = \pi - 2i$
Now the deviation is maximum when the value of i is minimum which occurs when $i = C$. Therefore, the maximum deviation possible is
$\delta = \pi - 2C$

So, the correct answer is “Option C”.

Note: It should be noted that total internal reflection occurs when the value of angle of incidence is greater than the critical angle for that medium. This is the reason why the minimum possible value of i is equal to the critical angle.