Question

A ray of light suffers minimum deviation, while passing through a prism of refractive index $1.5$ and refracting angle ${{60}^{0}}$. Calculate the angle of deviation and angle of incidence.

Answer 1

- Hint: This problem can be solved by using the direct formula for the angle of minimum deviation in terms of the angle of refraction and the refractive index of the material of the prism. The angle of incidence can then be found out using the direct formula in terms of the angle of deviation and the refracting angle.

Formula used:
$n=\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$
$i=\dfrac{A+{{\delta }_{m}}}{2}$

Complete step-by-step solution -
Let us use the direct formula for the angle of minimum deviation while refraction through a prism in terms of the refracting angle and the refractive index of the material of the prism.
The angle of minimum deviation ${{\delta }_{m}}$, the refracting angle $A$ of the prism and the refractive index $n$ of the material of the prism, when a light ray suffers minimum deviation when passing through the prism is given by
$n=\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$ --(1)
When a light ray passes through a prism, the angle of incidence $i$, the angle of deviation $\delta$ and the refracting angle $A$ are related as
$i=\dfrac{A+{{\delta }_{{}}}}{2}$ --(2)
Now, let us analyze the question.

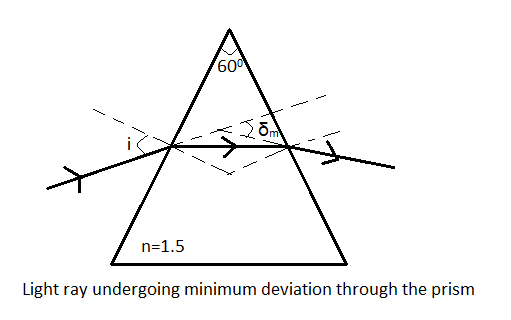
The refractive index of the material of the prism is $n=1.5$.
The refracting angle of the prism is $A={{60}^{0}}$.
Since, the ray suffers minimum deviation, let the angle of deviation be ${{\delta }_{m}}$.
Let the angle of incidence be $i$.
Using (1), we get
$n=\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$ --(3)
Putting the values of the variables in the above equation, we get
$1.5=\dfrac{\sin \left( \dfrac{{{60}^{0}}+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{{{60}^{0}}}{2} \right)}=\dfrac{\sin \left( \dfrac{{{60}^{0}}+{{\delta }_{m}}}{2} \right)}{\sin \left( {{30}^{0}} \right)}=\dfrac{\sin \left( \dfrac{{{60}^{0}}+{{\delta }_{m}}}{2} \right)}{\dfrac{1}{2}}$ $\left( \because \sin {{30}^{0}}=\dfrac{1}{2} \right)$
$\Rightarrow 1.5\times \dfrac{1}{2}=0.75=\sin \left( \dfrac{{{60}^{0}}+{{\delta }_{m}}}{2} \right)$
$\Rightarrow {{\sin }^{-1}}\left( 0.75 \right)=\dfrac{{{60}^{0}}+{{\delta }_{m}}}{2}$
$\Rightarrow {{48.6}^{0}}=\dfrac{{{60}^{0}}+{{\delta }_{m}}}{2}$ $\left( \because {{\sin }^{-1}}\left( 0.75 \right)\approx {{48.6}^{0}} \right)$
$\Rightarrow {{48.6}^{0}}\times 2={{60}^{0}}+{{\delta }_{m}}$
$\Rightarrow {{97.2}^{0}}={{60}^{0}}+{{\delta }_{m}}$
$\Rightarrow {{\delta }_{m}}={{97.2}^{0}}-{{60}^{0}}={{37.2}^{0}}$ --(3)
Therefore, we have got the required angle of deviation.
Now, we will try to find the angle of incidence.
Using (2), we get
$i=\dfrac{A+{{\delta }_{m}}}{2}$ --(4)
Using (3) and putting the values of the variables in the above equation, we get
$i=\dfrac{{{60}^{0}}+{{37.2}^{0}}}{2}=\dfrac{{{97.2}^{0}}}{2}={{48.6}^{0}}$
Therefore, we have got the required angle of incidence.

Note: Students must note that in use of formula (1), the refractive index of the medium should be replaced by the relative refractive index of the material of the prism to the refractive index of the medium if the prism is kept in some other medium with a refractive index different to that of air (which has a refractive index of 1). Here we assume that the prism has been kept in air and so we can directly use the refractive index of the material of the prism, that is, glass.