Question
Question: A ray of light strikes a plane mirror at an angle of incidence \({{45}^{\circ }}\) as shown in the f...
A ray of light strikes a plane mirror at an angle of incidence 45∘ as shown in the figure. After reflection, the ray passes through a prism of refractive index 1.5 whose apex angle is 4∘. Through what angle in degree must the mirror be rotated if the total deviation of the ray be 90∘?
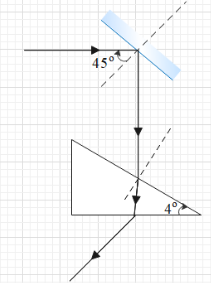
Solution
Use the formula for the angle of deviation when the light ray is incident on a plane mirror. Observe that the prism is a thin prism and use the formula for the angle of deviation due to a thin prism. Add them and find the angle of incidence on the mirror for the given total deviation.
Formula used:
δm=(180∘−2i)
where δm is the angle of deviation of the light ray when the angle of incidence is i on a plane mirror.
δp=(μ−1)A
where δp is the angle of deviation of light ray when is incidence on a thin prism, A is the angle of the prism and μ is the refractive index of the prism.
Complete step by step answer:
The angle of deviation of a ray of light that is incident on a mirror is given to be equal to δm=(180∘−2i).It is given that after reflection, the ray of light passes through a prism. Here, the prism is a thin prism since its angle is less that 5∘.Therefore, the angle by which the light ray deviates further after passing through the prism is equal to δp=(μ−1)A ….. (ii)
It is given that μ=1.5 and A=4∘.Substitute these values in equation (ii).
⇒δp=(1.5−1)(4)=2∘
This means that the angle of deviation in the light ray due to the prism is equal to 2∘. The total angle of deviation due to the mirror and the prism is equal to,
δ=δm+δp
Then,
⇒δ=(180∘−2i)+2∘ …. (iii)
However, it is said that the total angle of deviation of the light ray must be 90∘, i.e. δ=90∘.
With this, equation (iii) will change to 90∘=(180∘−2i)+2∘
⇒180∘−2i=88∘
⇒i=2180∘−88∘ ∴i=46∘
This means that for the light ray to go under a deviation of 90∘, the angle of incidence on the mirror must be equal to 46∘.But the initial angle of incidence is equal to 45∘.
Therefore, the mirror must be rotated by 46∘−45∘=1∘ for the required deviation.
Note: Note that for thin prisms, the angle of deviation is almost constant for all value of angle of incidence on the surface of the prism. Therefore, the deviation does not depend on the angle of incidence.However, for other prisms, the angle of deviation depends on the angle of incidence.
