Question
Question: A ray of light strikes a plane mirror at an angle of incidence \(45^\circ \)as shown in fig. 1.364. ...
A ray of light strikes a plane mirror at an angle of incidence 45∘as shown in fig. 1.364. After reflection, the ray passes through a prism of reflection index 1.5 whose apex angle is4∘. If the mirror is rotated by x∘then the total deviation of the ray becomes 90∘. Find x
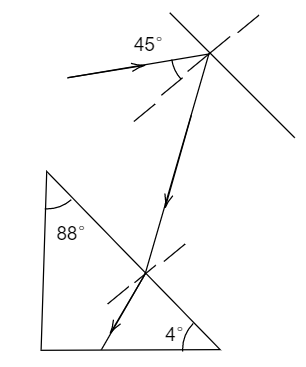
Solution
When there are many optical instruments involved then the total angle of deviation will be the sum of the angle of deviation of every optical instrument. The angle of the prism and apex angle represent the same thing which is the topmost angle of the prism.
Formula used:
For mirror
δ=180∘−2i
For prism with small apex angle
δ=A(n−1)
Where δ is the angle of deviation, Ais the apex angle,i is the angle of incidence, andn is the refractive index of prism.
Complete step-by-step answer:
For the initial case when the angle of incidence on mirror is 45∘(before rotation)
We know that,
For mirror
δ=180∘−2i
For prism with small apex angle
δ=A(n−1)
Where δ is the angle of deviation, Ais the apex angle,i is the angle of incidence, andn is the refractive index of prism.
Hence
The angle of deviation of ray due to mirror be δ1
⇒δ1=180∘−2(45∘)
⇒δ1=90∘
The angle of deviation of ray due to prism be δ2
It is given that the apex angle is4∘ and the refractive index of the prism is 1.5
⇒δ2=4(1.5−1)
⇒δ2=2∘
Let the total angle of deviation be δ3
We know that the total angle of deviation from the given setup will be δ1+δ2
⇒δ3=δ1+δ2
⇒δ3=90∘+2∘
⇒δ3=92∘
Now solving for the second case
For the second case when the mirror is rotated by x∘(let’s assume that we have turned the mirror in an anticlockwise direction) hence angle of incidence upon the mirror is (45+x)∘
We know that,
For mirror
δ=180∘−2i
For prism with small apex angle
δ=A(n−1)
Where δ is the angle of deviation, Ais the apex angle,i is the angle of incidence, andn is the refractive index of prism.
Hence
The angle of deviation of ray due to mirror be δ1
⇒δ1=180∘−2((45+x)∘)
⇒δ1=(90−2x)∘
The angle of deviation of ray due to prism be δ2
It is given that the apex angle is4∘ and the refractive index of the prism is 1.5
⇒δ2=4(1.5−1)
⇒δ2=2∘
Let the total angle of deviation be δ3 and it’s given that in this case δ3=90∘
We know that the total angle of deviation from the given setup will be δ1+δ2
⇒δ3=δ1+δ2
⇒δ3=(90−2x)∘+2∘
⇒90∘=(92−2x)∘
⇒2x=2
⇒x=1∘
As the value of xis positive our assumption of anticlockwise rotation was correct.
Therefore the correct answer to the above question is 1∘in an anticlockwise direction.
Note:
When the apex angle of the prism is small then we can use the trigonometric approximation which is sinθ≈θ. Due to this, the formula derived for the angle of deviation of the prism is independent of the angle of incidence which made our solution simpler.
