Question

A ray of light strikes a glass slab of thickness $t$ . It emerges on the opposite face, parallel to the incident ray but laterally displaced. Find the lateral displacement.
A) $0$
B) $t\sin \left( {i - r} \right)\cos r$
C) $t\dfrac{{\sin i}}{{\cos r}}$
D) $t\dfrac{{\sin \left( {i - r} \right)}}{{\cos r}}$

Answer 1

When a light ray enters from a rarer medium into a denser medium, the refracted ray will bend towards the normal. Here glass is denser than air. Sketching a ray diagram will provide a better understanding. The lateral displacement can be obtained by using simple rules of trigonometry for right-angled triangles formed by the refracted ray and the ray parallel to the incident ray.

Formulas used:
-The relation for the cosine of an angle in a right-angled triangle is given by, $\cos \theta = \dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$
-The relation for the sine of an angle in a right-angled triangle is given by, $\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$

Complete step by step answer.
Step 1: Sketch a ray diagram depicting the incidence and emergence of light from the glass slab.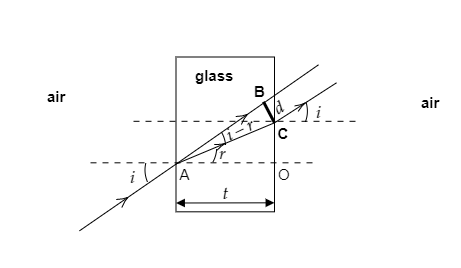

The above figure shows how the ray of light is incident on the glass slab of thickness $t$ and how it emerges from the slab to be parallel to the incident ray but suffering a lateral displacement $d$ .
The angle of incidence is marked as $i$ and the angle of refraction is marked as $r$ .
From the figure we also have $\angle BAC = i - r$ .
The side AO corresponds to the thickness of the slab.
i.e., $AO = t$
As seen from the figure the side BC will correspond to the lateral displacement of the emerging ray.
i.e., $BC = d$
Step 2: Obtain the sine and cosine of $\angle i - r$ and $\angle r$ in $\Delta ABC$ and $\Delta AOC$ to determine the lateral displacement $d$ .
Consider $\Delta AOC$ , we have $\cos r = \dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$
Here the adjacent side is $AO = t$ and the hypotenuse is ${\text{AC}}$ .
Then we have $\cos r = \dfrac{t}{{AC}}$
$\Rightarrow AC = \dfrac{t}{{\cos r}}$ --------- (1)
Consider $\Delta ABC$ , we have $\sin \left( {i - r} \right) = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$
Here the opposite side is $BC = d$ and the hypotenuse is ${\text{AC}}$ .
Then we have $\sin \left( {i - r} \right) = \dfrac{d}{{AC}}$--------- (2)
Substituting equation (1) in (2) we get, $\sin \left( {i - r} \right) = \dfrac{{d\cos r}}{t}$
$\Rightarrow d = t\dfrac{{\sin \left( {i - r} \right)}}{{\cos r}}$
Thus the lateral displacement is obtained as $d = t\dfrac{{\sin \left( {i - r} \right)}}{{\cos r}}$
So the correct option is D.

Note: The trigonometric relations for the sine and cosine of an angle can only be applied when dealing with a right triangle. Here both triangles $\Delta ABC$ and $\Delta AOC$ are right triangles and so we can apply these relations to find the lateral displacement. In $\Delta AOC$ , $\angle OF = 90^\circ$ and in $\Delta ABC$ , $\angle B = 90^\circ$ .