Question

A ray of light passing through the point $A{\text{ }}\left( {1,{\text{ }}2} \right)$ is reflected at a point B on the x−axis line mirror and then passes through $\left( {5,{\text{ }}3} \right)$ . Then the equation of AB is
A) $5x + 4y = 13$
B) $5x - 4y = - 3$
C) $4x + 5y = 14$
D) $4x - 5y = - 6$

Answer 1

Hint When a light is reflected from a plane line mirror, the angle of incidence will be equal to the angle of reflection. Using the equation of a line passing through two points we can determine the equation of $\overleftrightarrow {AB}$ .
Equation of line passing through two points: $y - {y_1} = m(x - {x_1})$ where ${x_1},{y_1}$ are the coordinates of one of the points on the line
Slope of a line passing through two points: $m = \tan \theta = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ where $\theta$ is the angle formed by the line of a line joining two points $({x_1},{y_1})$ and $({x_2},{y_2})$ , with the x-axis.

Complete step by step answer

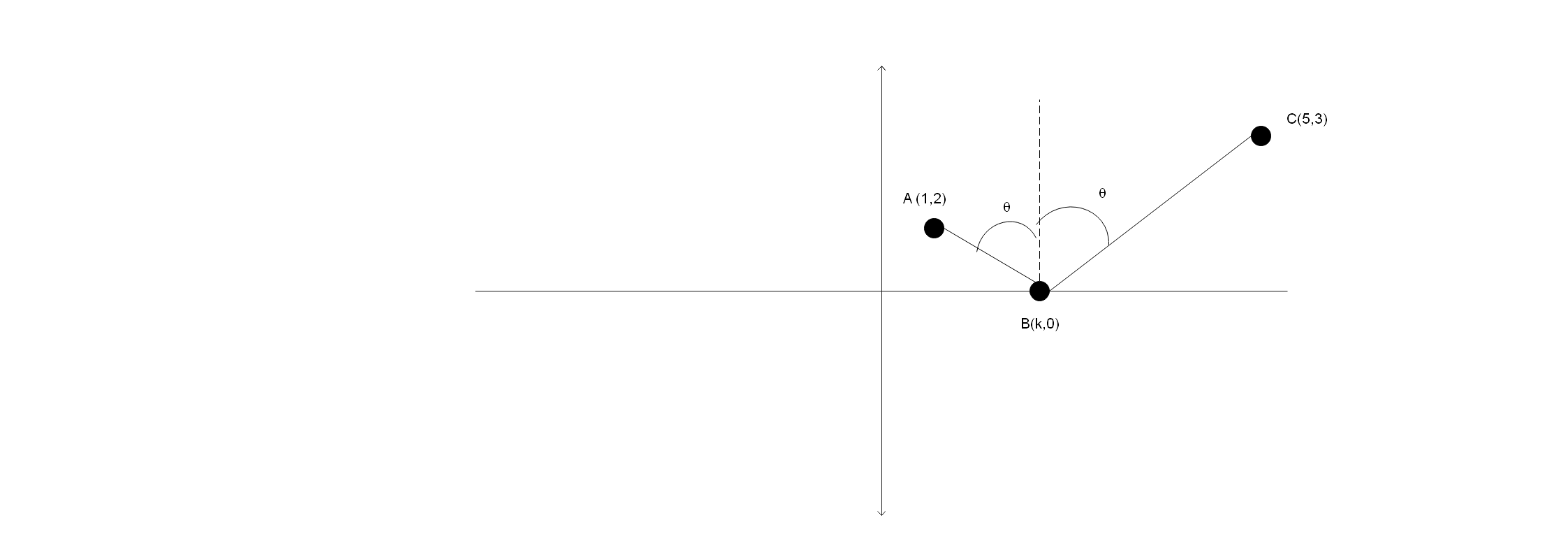
We know that point B is on the $x$ -axis so its $y$ -coordinate will be zero. Let us assume the coordinates of point B as $(k,0)$ .
Now for a reflection from a plane line mirror I.e. the $x$ -axis, we know that the angle of incidence is equal to the angle of reflection. The angle of incidence can be determined from the slope of the line joining points A and B. We know that the slope of a line joining two points $({x_1},{y_1})$ and $({x_2},{y_2})$ can be calculated as
$m = \tan \theta = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ where $\theta$ is the angle formed by the line with the x-axis
Since the angle of line AB w.r.t. the $x$ -axis is $180^\circ - \theta$ :
$\tan (180^\circ - \theta ) = \dfrac{{0 - 2}}{{k - 1}}$
As $\tan (180^\circ - \theta ) = - \tan \theta$ , we can write
$\tan \theta = \dfrac{2}{{k - 1}}$ (1)
Similarly, we can calculate the slope of the reflected ray formed by the line joining points B and C as
$\tan \theta = \dfrac{{3 - 0}}{{5 - k}}$
Comparing equations (1) and (2), we can write
$\dfrac{2}{{k - 1}} = \dfrac{{3 - 0}}{{5 - k}}$
Cross multiplying the denominators, we get
$10 - 2k = 3k - 3$
Solving for $k$ , we get
$k = \dfrac{{13}}{5}$
Then the coordinates of point B is $(13/5,0)$
We calculated the slope of line AB as
$m = \tan \theta = \dfrac{{ - 2}}{{k - 1}}$
Substituting the value of $k = 13/5$ , we get the slope as
$m = \tan \theta = \dfrac{{ - 10}}{8} = \dfrac{{ - 5}}{4}$
The equation of a line joining the points A and B can be calculated using the line formula for joining two points as:
$y - {y_1} = m(x - {x_1})$ where ${x_1},{y_1}$ are the coordinates of point A
Substituting $m = - 5/4$ , ${x_1} = 1$ and ${y_1} = 2$ , we get
$y - 2 = - \dfrac{5}{4}(x - 1)$
$4y - 8 = - 5x + 5$
On simplifying, we get
$5x + 4y = 13$ which corresponds to option (A).

Note
The trick to solving this question is to realize that the angle of incidence will be equal to the angle of refraction and then using the geometry of the problem to find the slope. We can alternatively check the options after finding the coordinates for point B and substituting the coordinates of points A and B as the equation of the line passing through A and B must satisfy the coordinates of both A and B.