Question

A ray of light passing from a glass of water is incident on the glass water interface at ${{65}^{o}}$. If the critical angle for the pair of media is ${{63}^{o}}$:
A) The ray will emerge into the water with a deviation of ${{2}^{o}}$ from the normal.
B) The ray will be refracted into the water with a deviation of ${{2}^{o}}$
C) The ray will be totally internally reflected back into the glass with a deviation of ${{50}^{o}}$
D) The ray will be totally internally reflected back into the glass with a deviation of ${{2}^{o}}$

Answer 1

It is given in the question that the angle of incident is ${{65}^{o}}$ and the critical angle of the medium is ${{63}^{o}}$ hence we apply the simple principle that is when angle of incidence is greater than critical angle a ray will get totally reflected back.

Formula used:
$\delta +i+r={{180}^{o}}$

Complete step by step solution:

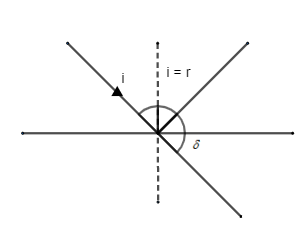
$\to$ Now it is given that in the question that the angle of incident is i = ${{65}^{o}}$
$\to$ And the critical angle of medium pair is c = ${{63}^{o}}$

$\to$ We know that when the angle of incident or incident angle (i) is greater than critical angle the ray will be reflected from glass as shown in the figure hence.
i > c
$\to$ So we can say that the incident angle will be equal to the reflection angle.
$i=r={{65}^{o}}....\left( 1 \right)$

$\to$Now in order to find the deviation $\left( \delta \right)$ we will use the below formula.
$\delta +i+r={{180}^{o}}......\left( 2 \right)$
$\delta$ = angle of deviation
i = angle of incident
r = angle of reflection

$\to$ Now substitute the value of equation (1) in equation (2) we will get
$\begin{aligned} & \Rightarrow \delta +{{65}^{o}}+{{65}^{o}}={{180}^{o}} \\\ & \Rightarrow \delta ={{180}^{o}}-{{130}^{o}} \\\ & \therefore \delta ={{50}^{o}} \\\ \end{aligned}$

$\to$ So the angle of the deviation is ${{50}^{o}}$ hence our correct answer will be option (c) the ray will be totally internally reflected back into glass with the deviation of ${{50}^{o}}$.

Note:
When ray will be reflected totally we can use below formula to find the angle of the deviation.
$\delta =180-2i$
$\delta$ = angle of deviation
i = angle of the incident.