Question

A ray of light making an angle $10^\circ$ with the horizontal is incident on a plane mirror making an angle $\theta$ with the horizontal. What should be the value of $\theta$ so that the reflected ray goes vertically upwards?
A. $20^\circ$
B. $30^\circ$
C. $40^\circ$
D. $50^\circ$

Answer 1

First draw the ray diagram of the given situation which shows the plane mirror, incident ray, normal to the mirror and reflected ray with all the angles. Use Snell's law of reflection to determine the angle made by the incident and reflected ray with the normal. Using the basic knowledge of the geometry, calculate the angle made by the mirror with the horizontal.

Complete step by step answer:
We have given that the ray of light is incident of a plane mirror making an angle of $10^\circ$ with the horizontal and the plane mirror making an angle of $\theta$ with the horizontal. We have asked that for what value of $\theta$, the reflected light from the mirror is perpendicular to the horizontal. Let us first draw the diagram of the rays incident and reflect it from the plane mirror.

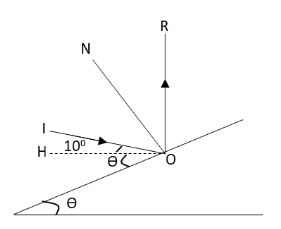
In the above ray diagram, I represent the incident ray, N represents the normal, R represents the reflected ray and H represents the horizontal. In the above diagram, the reflected ray is perpendicular to the horizontal. Hence, the angle between the horizontal and the reflected ray and horizontal is $90^\circ$. Thus, the angle between the reflected ray R and incident ray I is $90^\circ - 10^\circ = 80^\circ$.

According to Snell’s law of reflection, the incident ray and reflected ray makes the same angle with the normal.Hence, the angle made by the incident ray and reflected ray with the normal is $\dfrac{{80^\circ }}{2} = 40^\circ$.
$\angle {\text{ION}} = \angle {\text{NOR}} = 40^\circ$
The normal to the mirror is always perpendicular to the mirror. Hence, the angle made by the normal with the mirror is $90^\circ$. From the diagram, we can write
$\theta + \angle {\text{HOI}} + \angle {\text{ION}} = 90^\circ$
$\Rightarrow \theta + 10^\circ + 40^\circ = 90^\circ$
$\Rightarrow \theta + 50^\circ = 90^\circ$
$\Rightarrow \theta = 90^\circ - 50^\circ$
$\therefore \theta = 40^\circ$
Therefore, the value of the angle $\theta$ is $40^\circ$.

Hence, the correct option is C.

Note: The students should keep in mind that the reflected ray goes upward does not mean that the reflected ray is perpendicular to the plane mirror. It means that the reflected ray is perpendicular to the horizontal. Also the students should be careful while drawing the ray diagram and calculating the different angles.