Question

A ray of light making an angle ${10^\circ }$ with the horizontal is incident on a plane mirror making an angle $\theta$ with the horizontal. What should be the value of $\theta$ so that the reflected ray undergoes vertically upwards?
a. ${20^ \circ }$
b. ${30^\circ }$
c. ${40^\circ }$
d. ${50^\circ }$

Answer 1

The angle of reflection will be equal to the angle of incidence. And the angle of incidence, angle of reflection and the normal lies in the same plane. The normal will be perpendicular to the surface.

Complete step by step answer:
Given the angle between the ray of light and horizontal is ${10^\circ }$.
Usually the plane mirrors will have regular reflection. The image formed will be clear and visible. But the image cannot be focused on a screen. Hence we can call them virtual.

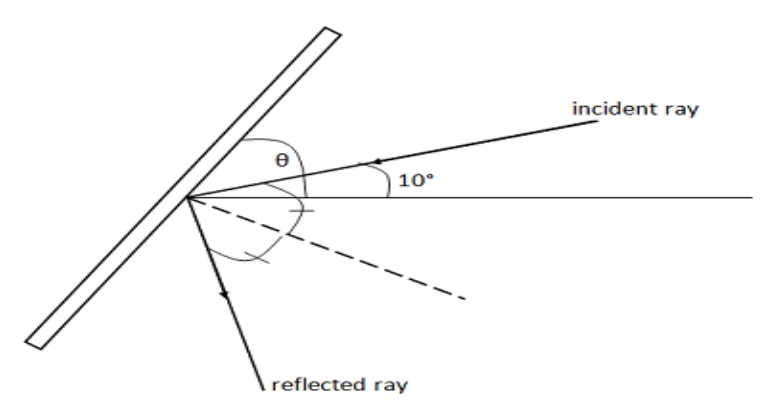
The angle between the reflected and incident ray can be calculated as,
${90^\circ } - {10^\circ } = {80^\circ }$
According to the law of reflection, the angle of incidence will be equal to angle of reflection.
And the angle of incidence, angle of reflection and the normal lies in the same plane.
Therefore, the angle of incidence= angle of reflection $= \dfrac{{{{80}^\circ }}}{2} = {40^\circ }$
The angle between the reflected ray with the mirror will be the perpendicular angle of the normal minus the angle of reflection.
Therefore, angle between the reflected ray with the mirror is ${90^\circ } - {40^\circ } = {50^\circ }$
Therefore the angle with the horizontal, $\theta = {90^\circ } - {50^\circ } = {40^\circ }$

Hence, the correct answer is option (C).

Note: We have to note that the angle of incidence and the angle of reflection is calculated by drawing a normal which is perpendicular to the surface of the plane mirror, and the angle of incidence or angle of reflected will be the angle between the normal and the ray.