Question

A ray of light makes an angle of $20^\circ$ with the horizontal and strikes a plane mirror which is inclined at an angle $\theta$ to the horizontal. The angle $\theta$ for which the reflected ray becomes vertical, is?
A. $40^\circ$
B. $80^\circ$
C. $35^\circ$
D. $100^\circ$

Answer 1

Use Snell’s law to determine the angle made by the incident and reflected rays with the normal. Use the law of alternate angles. Also, recall that the sum of all the angles in a right angle is $90^\circ$.

Complete step by step answer:
The ray of light is incident on a plane mirror by making an angle of $20^\circ$ with the horizontal. The plane mirror is inclined at angle $\theta$ to the horizontal.
The angle made by the incident ray and the reflected ray with normal is the same.
Draw the ray diagram for the light incident on the plane mirror.

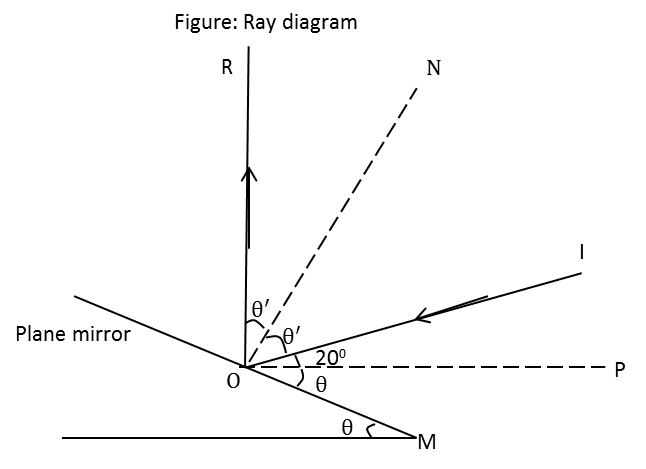
In the above ray diagram, ON is the normal, PO is the horizontal, OM is the plane mirror, IO is the incident ray on the plane mirror at an angle of $20^\circ$ with the horizontal, OR is the reflected ray, $\theta$ is the angle made by the plane mirror with the horizontal and $\theta '$ is the angle made by the incident and reflected rays with the normal.
According to the alternate angle theorem, the angle $\theta$ is equal to the angle POM.
The normal ON is perpendicular to the plane mirror. Hence, all the angles included in angle NOM (angle NOI, angle IOP and angle POM) is $90^\circ$.
$\angle {\text{NOM}} = 90^\circ$
$\angle {\text{NOI}} + \angle {\text{IOP}} + \angle {\text{POM}} = 90^\circ$
Substitute $\theta '$ for $\angle {\text{NOI}}$, $20^\circ$ for $\angle {\text{IOP}}$ and $\theta$ for $\angle {\text{POM}}$ in the above equation.
$\theta ' + 20^\circ + \theta = 90^\circ$
$\Rightarrow \theta ' + \theta = 90^\circ - 20^\circ$
$\Rightarrow \theta ' + \theta = 70^\circ$ …… (1)
The reflected ray becomes vertical. Hence, the reflected ray is perpendicular to the horizontal.
Hence, all the angles included in angle ROP (angle RON, angle NOI and angle IOP) is $90^\circ$.
$\angle {\text{ROP}} = 90^\circ$
$\angle {\text{RON}} + \angle {\text{NOI}} + \angle {\text{IOP}} = 90^\circ$
Substitute $\theta '$ for $\angle {\text{RON}}$, $\theta '$ for $\angle {\text{NOI}}$ and
$20^\circ$ for $\angle {\text{IOP}}$ in the above equation.
$\theta ' + \theta ' + 20^\circ = 90^\circ$
$\Rightarrow 2\theta ' + 20^\circ = 90^\circ$
$\Rightarrow 2\theta ' = 90^\circ - 20^\circ$
$\Rightarrow 2\theta ' = 70^\circ$
$\Rightarrow \theta ' = 35^\circ$
Hence, the angle made by the incident and reflected rays with the normal is $35^\circ$.
Substitute $35^\circ$ for $\theta '$ in equation (1).
$35^\circ + \theta = 70^\circ$
$\Rightarrow \theta = 70^\circ - 35^\circ$
$\Rightarrow \theta = 35^\circ$
Therefore, the angle made by the plane mirror with the horizontal is $35^\circ$.

So, the correct answer is “Option C”.

Note:
The alternate angles are the angle made by a line with the horizontal by joining to opposite ends of two parallel lines.
The angle made by the incident ray and the reflected ray with normal is the same.