Question
Question: A ray of light LM, incident normally on one face AB of a prism ABC having refracting angle \(A = 50^...
A ray of light LM, incident normally on one face AB of a prism ABC having refracting angle A=50∘ grazes the adjacent face AC (see Figure below). What is the refractive index of its material?
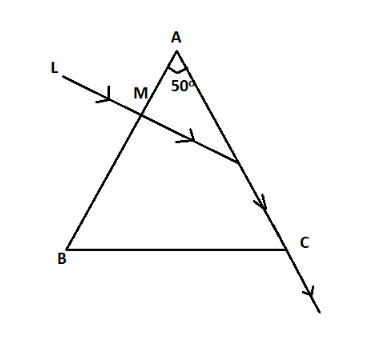
Solution
In order to solve this question you have to know the concept of the refractive index. Also you have to know the basic knowledge of maths. Also remember the relationship between the refractive index of the material and the angle of the prism.
Formula used:
The relationship between the refractive index and the angle of the prism
μ=sin(2A)sin(2A+δmin)
Where, μ is the refractive index of the material
A is the angle of the prism
δmin is the minimum angle of the deviation of the prism
Complete step by step solution:
Let us consider that the ray LM incident on the prism at point N.
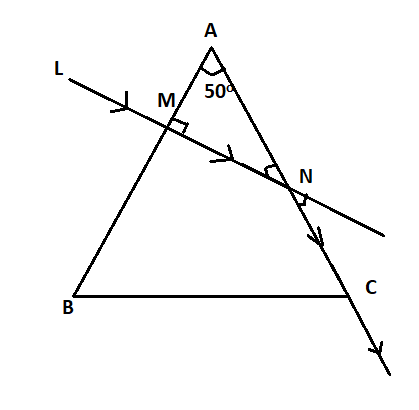
As we know that the sum of all the angles of a triangle is 180.
∠AMN+∠MAN+∠ANM=180∘
On putting the values, we get
⇒90+50+δmin=180
On further solving this, we have the angle of minimum deviation as
⇒δmin=40∘
Now, we know that the relationship between the refractive index and the angle of the prism is given by,
μ=sin(2A)sin(2A+δmin)
On putting all the values, we get
⇒μ=sin(250)sin(250+40)
On further solving this, we get the value of refractive index as,
⇒μ=1.673
Therefore, the refractive index of the material of prism is 1.673 .
Note: A prism is an optical object that is made up of a transparent material like plastic or glass, which has at least two flat surfaces that form an acute angle. A triangular prism can separate white light into its constituent colours, known as a spectrum. The angle between the two lateral faces of a prism is called the prism angle or the angle of prism.
