Question
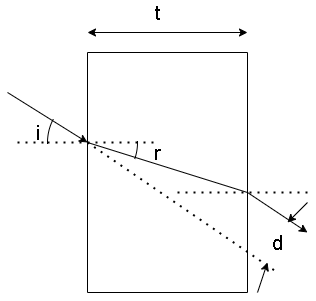
Question: A ray of light is incident on a thick slab of a glass of thickness t as shown in the figure. The eme...
A ray of light is incident on a thick slab of a glass of thickness t as shown in the figure. The emergent ray is parallel to the incident ray but displaced sideways by a distance d. If the angles are small then d is
A) T(1−ri)
B) Rt(1−ri)
C) it(1−ir)
D) T(i−r)
Solution
When the emergent ray is displaced then the phenomenon of lateral shift is observed. Lateral shift is the perpendicular distance between the incident ray and the emergent ray when the light ray undergoes refraction from a glass slab. The lateral displacement depends upon the thickness and the refractive index of the glass slab and the angle at which the incident ray enters the glass slab.
Formula used:
The formula of lateral displacement can be written as
D=cosrtsin(i−r)
Where D is the lateral displacement
t is the thickness of the slab
i is the angle of incidence
r is the angle of refraction
Complete step by step answer:
The ray of light incident on the glass slab undergoes refraction twice and comes out from the other side of the slab as an emergent ray.
The formula of lateral displacement D=cosrtsin(i−r)
Since the angle made by the incident and emergent ray, the angle is very small and when the angle is small then it can be written that
sin(i−r)≅i−r
And cosr≅1
Substituting the values in the formula, and solving for the value of lateral displacement
D=1t(i−r)
Taking ‘i’ common from the bracket, the equation reduces to the form
D=it(1−ir)
Therefore, Option C is the right answer.
Note:
It is to be noted that the emergent ray shows a lateral shift of the ray from the original path. When the Light is passing through the glass its velocity decreases but when it comes out of the glass slab, its velocity increases. The light ray then follows the same direction in the air.
