Question
Question: A ray of light is incident on a prism ABC of refractive index \(\sqrt3\) as shown in figure. (a)Fi...
A ray of light is incident on a prism ABC of refractive index 3 as shown in figure.
(a)Find the angle of incidence for which the deviation of light ray by the prism ABC is minimum.
(b) By what angle the second prism must be rotated, so that the final ray suffers net minimum deviation.
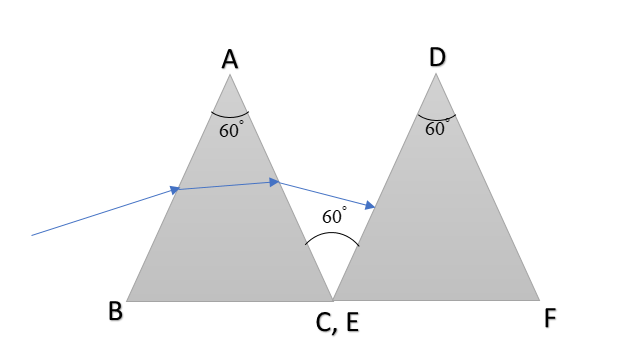
A.30∘, 60∘.
B.60∘, 30∘.
C.60∘, 60∘.
D.None.
Solution
A prism is not just an instrument. It’s basically a concept that could be applied when a light ray passes through a denser medium and gets out after suffering some deviation. Deviation of light ray is defined as the angle turned by the light ray after suffering refraction, measured with respect to the initial direction of light ray.
Formula used:
μ=sin(2A)sin(2A+δ)
Complete answer:
We have a well-known formula relating the angle of prism, minimum deviation and refractive index of the material of prism:
μ=sin(2A)sin(2A+δ)
Given; A=60∘ and μ=3
Hence we can use the relation. Putting all the known values in the relation, we get;
μ=sin(2A)sin(2A+δ)
⟹3=sin(260∘)sin(260∘+δmin)
⟹sin(260∘+δmin)=3×sin30∘=3/2
Hence, 260∘+δmin=60∘ [as sin 60∘=23]
⟹δmin=120∘−60∘=60∘
Now, for part (b) of the question, as the two prisms are symmetric, hence the deviation of the second prism will also be the same. Hence to minimize the net deviation from the combination of prisms, we need to place the prism such that the deviation produced from the first prism gets neutralized and hence becomes zero. Hence we have to turn the prism by 60∘, anticlockwise, as shown in the figure.
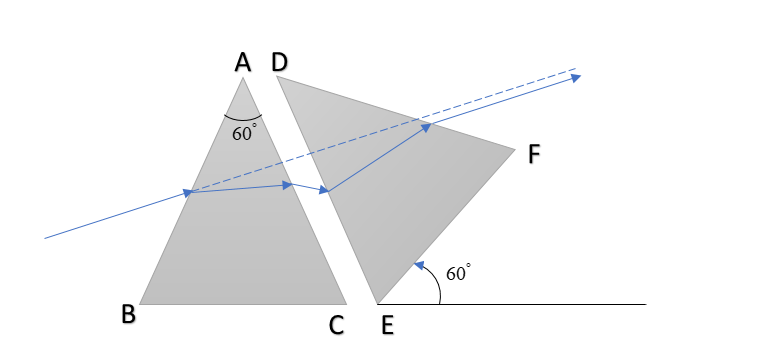
Hence, we can see that incident rays and the final transmitted rays are parallel and hence by definition, net deviation becomes zero.
So, the correct answer is “Option C”.
Note:
The angle of the prism is not always the angle of the top of the prism. This is a misconception, which needs to be removed. The angle of the prism is the angle which is opposite to the side, which is along the direction of incident ray. The relations used in prism analysis are derived by applying basic geometry and most importantly, Snell’s laws.
