Question

A ray of light is incident on a medium at an angle ‘i’. It is found that the reflected ray and refracted ray are perpendicular. What is the refractive index of the medium?

Answer 1

Here information about reflected ray and refracted rays are given, and we know that angle of reflection is equal to the angle of incident, so here we will use Snell's law for the determination of the refractive index of the medium. First, we will draw the given condition for a better understanding of the solution.

Complete step by step answer:
Let us assume that the refractive index of the medium is $\mu$.
In the question it is given that the reflected and refracted rays are perpendicular to each other, so we will draw the diagram of the given condition, as

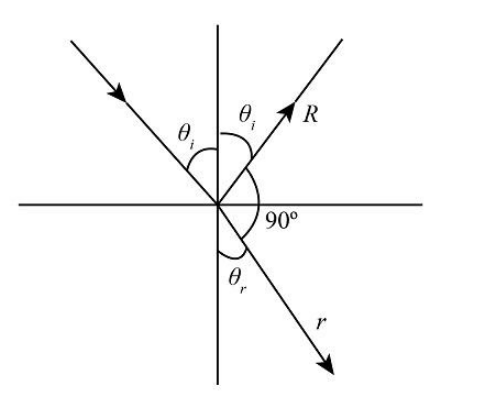
Here ${\theta _i}$ is the angle of incident and ${\theta _r}$ is the angle of refraction.

From the diagram we can say that the sum of the reflected angle, refracted angle and $90^\circ$ is $180^\circ$ and we know that the angle of incident and reflected angle are equal.
Therefore we get,
$\begin{array}{l} {\theta _i} + {\theta _r} + 90^\circ = 180^\circ \\\ {\theta _i} + {\theta _r} = 90^\circ \\\ {\theta _r} = 90^\circ - {\theta _i} \end{array}$…… (1)
Now we will use Snell’s law for the calculation of the refractive index.
$\mu = \dfrac{{\sin {\theta _i}}}{{\sin {\theta _r}}}$…… (2)
From equation (1) and (2), we get

\mu = \dfrac{{\sin {\theta _i}}}{{\sin 90^\circ - {\theta _i}}}\\\ \mu = \dfrac{{\sin {\theta _i}}}{{\cos {\theta _i}}}\\\ \mu = \tan {\theta _i} \end{array}$$ Therefore, if a ray of light is incident on a medium at an angle ‘i’, it is found that the reflected ray and refracted ray are perpendicular. The refractive index of the medium is $$\tan {\theta _i}$$. **Note:** In this question, the only relation between the reflected ray and refracted ray is given, but in these type of question if the values of the incident, reflected and refracted angles are given then apply these values directly in the Snell’s law formula and determine the refractive index in numerical value.