Question

A ray of light is incident at $60^\circ$ on a prism of refracting angle $30^\circ$ . The emerging ray is at an angle $30^\circ$ with the incident ray. The value of the refractive index of the prism is?
(A) $\dfrac{{\sqrt 3 }}{4}$
(B) $\dfrac{{\sqrt 3 }}{2}$
(C) $\sqrt 3$
(D) $\dfrac{2}{{\sqrt 3 }}$

Answer 1

Hint : In this question, we have to use the concept of refraction of light when it passes through a prism. The refractive index is a measure of comparing different materials. It tells how fast light can travel through a medium. Since ${\delta _m}$ is not given so we cannot use the formula $\mu = \dfrac{{\sin (A + \dfrac{{{\delta _m}}}{2})}}{{\sin (\dfrac{A}{2})}}$ . Instead find ${r_1}$ and use the formula $\mu = \dfrac{{\sin {i_1}}}{{\sin {r_1}}}$ , since ${i_1}$ is given.

Complete Step By Step Answer:
Given are the following information: Incident angle ${i_1} = 60^\circ$ , Angle of prism $A = 30^\circ$ , Angle of deviation(angle between incident ray and emergent ray) $\delta = 30^\circ$ . Let the emergent angle be ${i_2}$ , refractive angle at incident plane ${r_1}$ and refractive angle at emergent plane ${r_2}$ as shown in the figure-

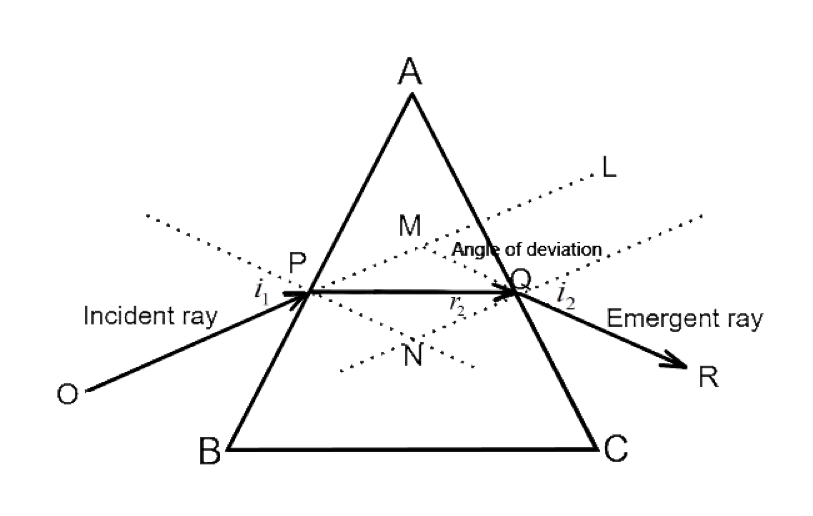
From the figure we note that ${i_1} = {r_1} + {\delta _1}$ and ${i_2} = {r_2} + {\delta _2}$ . Adding both equations we have
${i_1} + {i_2} = {r_1} + {r_2} + {\delta _1} + {\delta _2}$ (1)
From $\vartriangle PMQ$ and $\square APNA$ we see that $\delta = {\delta _1} + {\delta _2}$ and $A = {r_1} + {r_2}$ respectively
Substituting this and respective values of variables in equation 1, we get,
${i_1} + {i_2} = A + \delta \Rightarrow {i_2} = 0^\circ$
which further implies that
${r_2} = 0^\circ \Rightarrow {r_1} = A = 30^\circ$
Using Snell’s law $\mu = \dfrac{{\sin {i_1}}}{{\sin {r_1}}} \Rightarrow \mu = \dfrac{{\sin 60^\circ }}{{\sin 30^\circ }} \Rightarrow \mu = \sqrt 3$
Therefore, the refractive index of the prism $\mu = \sqrt 3$ .
The answer is option (C).

Note :
Don’t get confused by the term refracting angle. It is not the refractive angle at the incident plane. The angle of prism A is also called refracting angle. Also, whenever it is mentioned the angle made by emergent ray with incident ray it means the total deviation $\delta ( = {\delta _1} + {\delta _2})$ .