Question

A ray of light is incident along a line which meets another line $7x - y + 1 = 0$, at the point (0,1). The ray is then reflected from this point along the line $y + 2x = 1$. What is the equation of the line of incidence of the ray of light?
${\text{A}}{\text{. }}41x - 25y + 25 = 0 \\\ {\text{B}}{\text{. }}41x + 25y - 25 = 0 \\\ {\text{C}}{\text{. }}41x + 38y - 38 = 0 \\\ {\text{D}}{\text{. }}41x - 38y + 38 = 0 \\\$

Answer 1

Hint: Here, we will proceed by using the law of reflection that the angle of incidence is always equal to the angle of reflection and then use the formula $\tan \theta = \left| {\dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}} \right|$ to evaluate the slope of the incident ray of light.

Complete step-by-step answer:
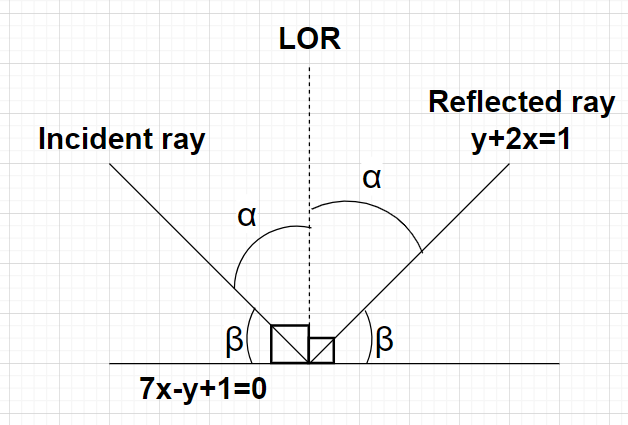
Given, equation of the reflected ray of light is $y + 2x = 1$
Let m be the slope of the incident ray of light.
Let $\alpha$ be the angle of incidence of the incident ray of light as shown in the figure.
Therefore, the angle between the incident ray of light and the line $7x - y + 1 = 0$ will be equal to $\left( {{{90}^0} - \alpha } \right) = \beta$ (say).
Clearly, the perpendicular to the line $7x - y + 1 = 0$ is the line of reference (LOR).
According to laws of reflection, we know that the angle of incidence of the ray of light is equal to the angle of reflection of the ray of light. So, the angle of the reflection of the reflected ray of light $y + 2x = 1$ will also be equal to $\alpha$ as shown in figure.
Also, the angle between the reflected ray of light $y + 2x = 1$ and the line $7x - y + 1 = 0$ will also be equal to $\left( {{{90}^0} - \alpha } \right) = \beta$.
Since, the angles made by the incident ray of light and the reflected ray of light with the line $7x - y + 1 = 0$ are same (i.e., $\left( {{{90}^0} - \alpha } \right) = \beta$).
As we know that angle between two lines whose slopes are ${m_1}$ and ${m_2}$ is given by $\tan \theta = \left| {\dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}} \right|$
Any general equation of line is given by $y = mx + c \\\ \Rightarrow mx - y + c = 0{\text{ }} \to {\text{(1)}} \\\$ where m is the slope of the line and c is the y intercept of the line.
So, the angle between the incident ray of light whose slope is m and the line $7x - y + 1 = 0$ whose slope is 7 will be equal to the angle between the reflected ray of light $y + 2x = 1 \\\ \Rightarrow - 2x - y + 1 = 0 \\\$ whose slope is -2 and the line $7x - y + 1 = 0$ whose slope is 7.
i.e., $\left| {\dfrac{{m - 7}}{{1 + 7m}}} \right| = \left| {\dfrac{{ - 2 - 7}}{{1 + \left( { - 2} \right)\left( 7 \right)}}} \right| \\\ \Rightarrow \left| {\dfrac{{m - 7}}{{1 + 7m}}} \right| = \left| {\dfrac{{ - 9}}{{1 - 14}}} \right| = \left| {\dfrac{{ - 9}}{{ - 13}}} \right| \\\ \Rightarrow \left| {\dfrac{{m - 7}}{{1 + 7m}}} \right| = \dfrac{9}{{13}} \\\$
Either $\dfrac{{m - 7}}{{1 + 7m}} = \dfrac{9}{{13}} \\\ \Rightarrow 13\left( {m - 7} \right) = 9\left( {1 + 7m} \right) \\\ \Rightarrow 13m - 91 = 9 + 63m \\\ \Rightarrow 50m = - 100 \\\ \Rightarrow m = - 2 \\\$ or $\dfrac{{m - 7}}{{1 + 7m}} = - \dfrac{9}{{13}} \\\ \Rightarrow 13\left( {m - 7} \right) = - 9\left( {1 + 7m} \right) \\\ \Rightarrow 13m - 91 = - 9 - 63m \\\ \Rightarrow 76m = 82 \\\ \Rightarrow m = \dfrac{{82}}{{76}} = \dfrac{{41}}{{38}} \\\$
So, the slope of the incident ray of light is either -2 or $\dfrac{{41}}{{38}}$.
Equation of the incident ray of light can be written using equation (1) as $mx - y + c = 0$
When m=-2, equation of the incident ray of light becomes $- 2x - y + c = 0$
When m=$\dfrac{{41}}{{38}}$, equation of the incident ray of light becomes $\dfrac{{41x}}{{38}} - y + c = 0$
Since, the incident ray of light meets the line $7x - y + 1 = 0$ at a point (0,1) which means this point will satisfy the equation of the incident ray of light.
For the equation of the incident ray of light as $- 2x - y + c = 0$,
$\Rightarrow \left( { - 2 \times 0} \right) - 1 + c = 0 \\\ \Rightarrow c = 1 \\\$
Hence, the equation of the incident ray of light is $- 2x - y + 1 = 0$ which is not there in the options.
For the equation of the incident ray of light as $\dfrac{{41x}}{{38}} - y + c = 0$,
$\Rightarrow \dfrac{{\left( {41 \times 0} \right)}}{{38}} - 1 + c = 0 \\\ \Rightarrow c = 1 \\\$
Hence, the equation of the incident ray of light is $\dfrac{{41x}}{{38}} - y + 1 = 0 \\\ \Rightarrow \dfrac{{41x - 38y + 38}}{{38}} = 0 \\\ \Rightarrow 41x - 38y + 38 = 0 \\\$
Hence, option D is correct.

Note: In this particular problem, there are two equations of the incident ray of light which can be possible i.e., $- 2x - y + 1 = 0$ and $41x - 38y + 38 = 0$ but here only $41x - 38y + 38 = 0$ is considered because of the options given in the problem.