Question

A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in fig. What must be the minimum value of the refractive index of glass? Give relevant calculations.

Answer 1

For total internal reflection (TIR), the angle of incidence must be greater than or equal to the critical angle $C$ . Also, the light must be travelling from a denser medium to a rarer medium. In the above question, light travels from glass towards the air. At the glass air junction, instead of getting refracted, it gets reflected.

Formulae used:
$\mu = \dfrac{1}{{\sin C}}$ where $\mu$ is the refractive index of the medium and $C$ is the critical angle at which total internal reflection occurs .

Complete step by step answer:

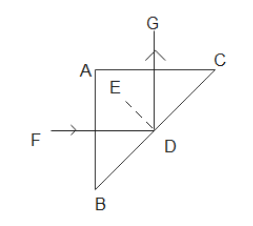
According to the given question , triangle ABC is an isosceles triangle, where
$\angle BAC = 90^\circ$
$\Rightarrow \angle ABC = \angle ACB = 45^\circ$
Since the light is incident normally on the face of the prism, we have
$\angle BDF = 45^\circ$
Let $DE$ be the normal at $BDG$ ,
Therefore ,
$\angle FDE = \angle EDG = 45^\circ$

Now, applying the formula $\mu = \dfrac{1}{{\sin C}}$ , we get,
$\mu = \dfrac{1}{{\sin 45^\circ }}$
where $\mu$ is the refractive index of the prism and angle of incidence at point $D$ is $45^\circ$ which is given to be the critical angle.
Hence, we have
$\mu = \dfrac{1}{{\sin 45^\circ }} \\\ \Rightarrow \mu = \sqrt 2 \\\ \therefore \mu = 1.414$

Therefore, the minimum value of the refractive index of glass must be 1.414 for total internal reflection (TIR) to take place.

Note: Many students commit the blunder of taking $90^\circ$ as the angle of incidence. You must remember that the angle of incidence for total internal reflection (TIR) should be the angle at which the light is striking the glass air interface. In simple words, the angle at which light travels from glass to just strike the air should be considered an angle of incidence.