Question

A ray of light incident normally on one face of a glass prism of refractive index $\sqrt 2$ and just emerges from another face. Find the angle of the prism.

Answer 1

A prism is an optical device which is made with precise angle and it is used for analyzing the reflecting lights. The prism can also be used for separating the light into its constituent colours which is known as spectrum.

Formula used: The formula of the Snell’s law is given by,
$\Rightarrow {n_1}\sin i = {n_2}\sin r$
Where refractive index of the two mediums are${n_1}$,${n_2}$ and angle of incidence is i and the angle of refraction is r.

Complete step by step solution:
It is given in the problem that the light ray falling on the prism has refractive index $\sqrt 2$ and the fall is perpendicular to the surface and we need to find the angle of the prism if the apex angle is$30^\circ$.

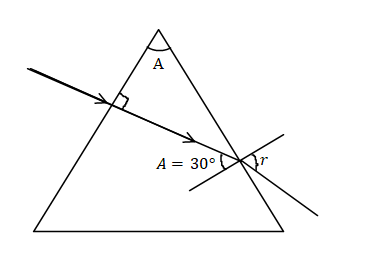
The angle of incidence for the prism is$90^\circ$, the refractive index is equal to $\sqrt 2$ and by applying the Snell’s law we can calculate the angle of refraction.
The formula of the Snell’s law is equal to,
$\Rightarrow {n_1}\sin i = {n_2}\sin r$
Where refractive index of the two mediums are${n_1}$,${n_2}$ and angle of incidence is i and the angle of refraction is r.
The refractive index of air is 1 and the refractive index of prism is$\sqrt 2$ applying these values in the Snell’s law we get.
$\Rightarrow {n_1}\sin i = {n_2}\sin r$
$\Rightarrow 1 \times \sin 90^\circ = \sqrt 2 \times \sin r$
$\Rightarrow \sin r = \dfrac{{\sin 90^\circ }}{{\sqrt 2 }}$
The value of $\sin 90^\circ$ is equal to 1.
$\Rightarrow \sin r = \dfrac{1}{{\sqrt 2 }}$
$\Rightarrow r = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$
The value of ${\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$ in angles is equal to$45^\circ$.
Therefore the value of angle of refraction is equal to,
$\Rightarrow r = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$
$\Rightarrow r = 45^\circ$.
The angle of refraction is equal to$r = 45^\circ$.

Note: The students are advised to understand and remember the formula of the Snell’s law as it is helpful in solving problems like these. The angle of the equilateral triangle is $30^\circ$ and therefore the prism has a vertex angle as $30^\circ$.