Question

A ray of light from a denser medium strikes a rarer medium at angle of incidence $i$. The reflected and refracted rays make an angle of ${90^ \circ }$ with each other. The angle of reflection and refraction are $r$ and $r'$. The critical angle is
(A) ${\sin ^{ - 1}}\left( {\tan r} \right)$
(B) ${\sin ^{ - 1}}\left( {\tan i} \right)$
(C) ${\sin ^{ - 1}}\left( {\tan r'} \right)$
(D) ${\sin ^{ - 1}}\left( {\tan \left( {i + r} \right)} \right)$

Answer 1

To solve this question, we need to use the Snell’s law using which we can determine the refractive index of the denser medium with respect to the rarer medium. Then putting it into the formula for the critical angle we will get the final answer.

Formula used: The formulae used for solving this question are given by
1. ${\mu _1}\sin i = {\mu _2}\sin r$, here ${\mu _1}$ and ${\mu _2}$ are the refractive indices of the first and the second medium, and $i$ and $r$ are the respective angles of incidence and refraction.
2. ${i_c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)$, here ${i_c}$ is the critical angle of incidence for a light which travels from a denser to a rarer medium, and $\mu$ is the refractive index of the denser medium with respect to the rarer medium.

Complete step-by-step solution:
Let the refractive index of the denser medium be ${\mu _d}$ and that of the rarer medium be ${\mu _r}$.
Now, the angle of incidence is given to be equal to $i$, the angle of reflection is $r$, and the angle of refraction is $r'$. So we represent this situation by the figure shown below.

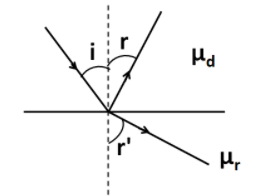
Now, from the given figure we can write
$r + {90^ \circ } + r' = {180^ \circ }$
$\Rightarrow r' = {90^ \circ } - r$...............(1)
Also, since we know that the angle of reflection is equal to the angle of incidence, so we can write
$i = r$ …………………...(2)
Now, we apply the Snell’s law for the refraction of the incident light from the denser to the rarer medium to get
${\mu _d}\sin i = {\mu _r}\sin r'$
Putting (1) and (2) in the above equation we get
${\mu _d}\sin r = {\mu _r}\sin \left( {{{90}^ \circ } - r} \right)$
$\Rightarrow {\mu _d}\sin r = {\mu _r}\cos r$
Dividing by ${\mu _r}\sin r$ on both the sides, we get
$\dfrac{{{\mu _d}}}{{{\mu _r}}} = \dfrac{{\cos r}}{{\sin r}}$
$\Rightarrow \dfrac{{{\mu _d}}}{{{\mu _r}}} = \cot r$
So the refractive index of the denser medium with respect to the rarer medium is given by
${\mu _{dr}} = \cot r$........................(3)
Now, we know that the critical angle is equal to the sine inverse of the reciprocal of the refractive index of the denser medium with respect to the rarer medium. So we have
${i_c} = {\sin ^{ - 1}}\left( {\dfrac{1}{{{\mu _{dr}}}}} \right)$
Putting (3) in the above equation we have
${i_c} = {\sin ^{ - 1}}\left( {\dfrac{1}{{\cot r}}} \right)$
$\Rightarrow {i_c} = {\sin ^{ - 1}}\left( {\tan r} \right)$
Thus, the critical angle for the given pair of the mediums is equal to ${\sin ^{ - 1}}\left( {\tan r} \right)$.

Hence, the correct answer is option A.

Note: We must note that the refractive index appearing in the formula for the critical angle is the relative refractive index of denser medium with respect to the rarer medium. It is not the refractive index with respect to the air.