Question

A ray of light falls on the surface of a spherical glass paperweight making an angle $\alpha$ with the normal and is refracted in the medium at an angle $\beta$. The angle of deviation of the emergent ray from the incident ray is
a) $\left( \alpha -\beta \right)$
b) $2\left( \alpha -\beta \right)$
c) $\dfrac{\left( \alpha -\beta \right)}{2}$
d) $\left( \alpha +\beta \right)$

Answer 1

In the above question we are asked to determine the angle of deviation that is the angle between the incident ray and the emergent ray coming out of the a spherical glass. First we need to draw a diagram to understand how the rays of light propagate when it is incident on the spherical glass. Further accordingly looking at the figure we will be able to draw the diagram.

Complete answer:

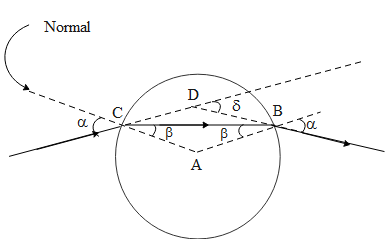
In the above figure the incident ray is traced till it emerges out of the spherical surface. The ray hits the spherical surface at C, then it moves into the glass and emerges out of the spherical surface at point B. The incident ray makes an angle $\alpha$ with the normal at C while the refracted ray makes an angle $\beta$ with the normal at C. The angle of emergence $\delta$ is the angle between the incident and the emergent ray.
From the above figure, AC = AB, as these two sides are the radius of the same circle. This implies that $\angle CBA=\angle BCA=\beta$ . Hence using the principle of reversibility of light, it also can be implied that angle of emergence is also $\alpha$ .
The exterior angle of a triangle is equal to the sum of the two opposite interior angles. Hence from the above figure, it can be concluded that,
$\delta =\angle DCB+\angle DBC....(1)$
But using the property of vertically opposite angle of a triangle we obtain,
$\angle DCB=\alpha -\beta$ and $\angle DBC=\alpha -\beta$
Hence using equation 1 we get the angle of deviation as,
$\begin{aligned} & \delta =\angle DCB+\angle DBC \\\ & \because \angle DCB=\angle DBC=\alpha -\beta \\\ & \Rightarrow \delta =\alpha -\beta +\alpha -\beta \\\ & \therefore \delta =2\left( \alpha -\beta \right) \\\ \end{aligned}$

Therefore the correct answer of the above question is option b.

Note:
The principle of reversibility of light states that if light travels from point of incidence to point of emergence, light traverses the same path again if it so happens that it travels vice versa. The angle of refraction had to be the same as angle of incidence at point B. The angle of emergence had to be equal to the angle of incidence at point C. This is due to the fact that the refractive index of the medium with respect to a common medium is always the same.