Question

A ray of light falls on a transparent sphere with center at C is shown in Fig. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

A. $\sqrt 2$
B. $\sqrt 3$
C. $\dfrac{3}{2}$
D. $\dfrac{1}{2}$

Answer 1

We can solve this equation using Snell’s law. Snell’s law states that the ratio of the sine of the incident angle and the angle of transmission is equal to the ratio of the refractive index of the material at surface. Calculate the angle of refraction and then use the formula of Snell’s law to find the refractive index.

Complete step by step answer:
We need to find the angle of refraction and then we can apply Snell’s law to calculate the value of the refractive index. In order to find the angle of refraction, we need to trace the ray as it enters the transparent surface and then leaves the surface. Let us draw an appropriate diagram for that:

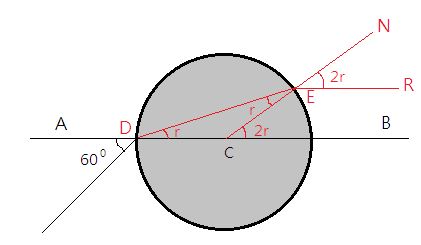
From Snell’s law we know that;
$\sin i = \mu \sin r$ --equation $A$
Here $i$ is the angle of incidence and $r$ is the angle of refraction.
C is the centre of the circle. Perpendicular to any point on the circle will pass through the centre. Thus, the normal at E, CN is a perpendicular to this circle.
We need to find the angles; $\angle EDC,\,\angle CED,\,\angle BCE$ in order to apply Snell’s law at various points.
CE and DC are the radius of the circle and CE, DC are the sides of $\vartriangle DCE$ and we know that the angles opposite of equal sides are equal. Therefore, we can have
$\angle EDC = \angle CED = r$ --equation $1$
Here, $r$ is the angle of refraction.
From exterior angle theorem, we have
$\angle BCE = 2r$ --equation $2$
Now, applying Snell’s law at point E, we have
$\mu \sin r = \sin 2r$
$\mu = \dfrac{{\sin 2r}}{{\sin r}}$ --equation $3$
using equation $A$ we know that
$\sin 2r = \sin i$
And angle $i = {60^ \circ }$
Therefore, we have $r = {30^ \circ }$
Applying this value in equation $3$ , we get
$\mu = \dfrac{{\sin (2 \times {{30}^ \circ })}}{{\sin ({{30}^ \circ })}}$
$\Rightarrow \mu = \dfrac{{\sin {{60}^ \circ }}}{{\sin {{30}^ \circ }}}$
$\Rightarrow \mu = \sqrt 3$
Therefore, the refractive index of the sphere is $\sqrt 3$

So, the correct answer is “Option B”.

Note:
Snell’s law states that the ratio of the sine of the incident angle and the angle of transmission is equal to the ratio of the refractive index of the material at surface.
It is easy to solve the question after drawing the diagram.
Also, remember that we need to use some trigonometric equations in this problem.