Question

A ray of light enters at grazing angle of incidence into an assembly of three isosceles right-angled prisms having refractive indices ${\mu _1} = \sqrt 2$,${\mu _2} = \sqrt x$ and ${\mu _3} = \sqrt 3$. If finally an emergent light ray also emerges at gazing angle then calculate x.

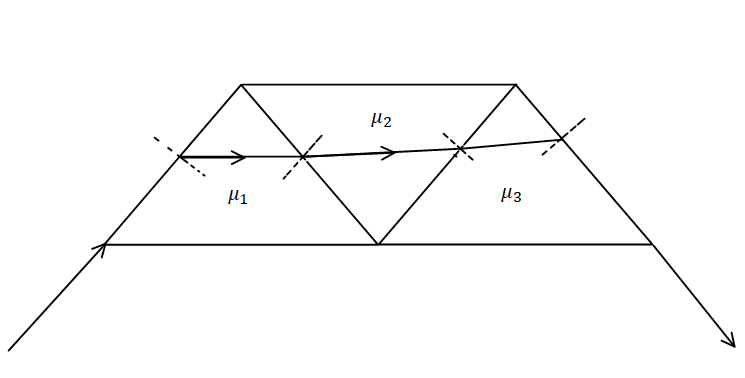
A) 5
B) 3
C) 2
D) 1

Answer 1

The speed of light is different in different mediums and due to which the when a ray of light enters from one medium into another medium then the ray of light bends from the normal to the medium also speed of light of the medium depends upon the refractive index of the respective medium.

Complete step by step answer:
The Snell’s law is given by,$\dfrac{{\sin {i_1}}}{{\sin {r_1}}} = {\mu _1}$
As the angle of incidence is$90^\circ$ as the refractive index of the air is 1.
$\Rightarrow \dfrac{{\sin {i_1}}}{{\sin {r_1}}} = {\mu _1}$
$\Rightarrow \sin {r_1} = \dfrac{{\sin {i_1}}}{{{\mu _1}}}$
$\Rightarrow \sin {r_1} = \dfrac{{\sin 90^\circ }}{{\sqrt 2 }}$(as the value of the ${i_1} = 90^\circ$)
$\Rightarrow \sin {r_1} = \dfrac{1}{{\sqrt 2 }}$(Since the value of $\sin 90^\circ$is equal to 1)
$\Rightarrow {r_1} = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$
$\Rightarrow {r_1} = 45^\circ$(as the angle of $\sin 45^\circ$ is equal to $\dfrac{1}{{\sqrt 2 }}$)
Applying the Snell’s law for the second surface,
$\Rightarrow \dfrac{{\sin {i_2}}}{{\sin {r_2}}} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
Since $\sin {i_2} = \cos {r_1}$
$\Rightarrow \dfrac{{\cos {r_1}}}{{\sin {r_2}}} = \dfrac{{{\mu _2}}}{{\sqrt 2 }}$(as the value of ${\mu _3} = \sqrt 2$)
$\Rightarrow \sqrt 2 \cos {r_1} = {\mu _2}\sin {r_2}$
$\Rightarrow \sin {r_2} = \dfrac{{\sqrt 2 }}{{{\mu _2}}} \cdot \left( {\cos 45^\circ } \right)$ (as the value of ${r_1} = 45^\circ$)
$\Rightarrow \sin {r_2} = \dfrac{1}{{{\mu _2}}}$………eq. (1)
Snell’s law for the third surface.
$\Rightarrow \dfrac{{\sin {i_3}}}{{\sin {r_3}}} = \dfrac{{{\mu _3}}}{{{\mu _2}}}$
$\Rightarrow \dfrac{{\sin {i_3}}}{{\sin {r_3}}} = \dfrac{{\sqrt 3 }}{{{\mu _2}}}$(as the value of ${\mu _3} = \sqrt 3$)
Since$\sin {i_3} = \cos {r_2}$, therefore we get
$\Rightarrow \dfrac{{\cos {r_2}}}{{\sin {r_3}}} = \dfrac{{\sqrt 3 }}{{{\mu _2}}}$
$\Rightarrow \sin {r_3} = \dfrac{{{\mu _2}\sqrt {1 - \sin {r_2}^2} }}{{{\mu _3}}}$ (Since $\cos {r_2} = \sqrt {1 - {{\sin }^2}{r_2}}$)
$\Rightarrow \sin {r_3} = \dfrac{{{\mu _2}\sqrt {1 - {{\left( {\dfrac{1}{{{\mu _2}}}} \right)}^2}} }}{{\sqrt 3 }}$(replacing the value of $\sin {r_2}$from equation (1))
$\Rightarrow \sin {r_3} = \dfrac{{{\mu _2}\sqrt {\dfrac{{{\mu _2}^2 - 1}}{{{\mu _2}^2}}} }}{{\sqrt 3 }}$(Taking L.C.M)
$\Rightarrow \sin {r_3} = \dfrac{{\sqrt {{\mu _2}^2 - 1} }}{{\sqrt 3 }}$………eq. (2)
For the fourth interface, Snell’s law would be,
$\Rightarrow \dfrac{{\sin {i_4}}}{{\sin {r_4}}} = \dfrac{{{\mu _4}}}{{{\mu _3}}}$
$\Rightarrow \dfrac{{\sin {i_4}}}{{\sin 90^\circ }} = \dfrac{1}{{\sqrt 3 }}$(As the value of ${r_4} = 90^\circ$ also the value of${\mu _3} = \sqrt 3$)
$\Rightarrow \sin {i_4} = \dfrac{1}{{\sqrt 3 }}$
Also,$\sin {i_4} = \cos {r_3}$,
$\Rightarrow \cos {r_3} = \dfrac{1}{{\sqrt 3 }}$………eq. (3)
We know that,
$\Rightarrow {\sin ^2}{r_3} + {\cos ^2}{r_3} = 1$
Replace the value of $\sin {r_3}$ and $\cos {r_3}$ from equation (2) and equation (3) in above equation.
$\Rightarrow {\sin ^2}{r_3} + {\cos ^2}{r_3} = 1$
$\Rightarrow {\left[ {\dfrac{{\sqrt {{\mu _2}^2 - 1} }}{{\sqrt 3 }}} \right]^2} + {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} = 1$
On simplification,
$\Rightarrow \dfrac{{{\mu _2}^2 - 1}}{3} + \dfrac{1}{3} = 1$
$\Rightarrow \dfrac{{{\mu _2}^2 - 1 + 1}}{3} = 1$
On further simplification,
$\Rightarrow \dfrac{{{\mu _2}^2}}{3} = 1$
$\Rightarrow {\mu _2} = \sqrt 3$

Therefore, the value of x=3. So the correct is option B.

Note:
It is advisable for the students to remember Snell’s law as it is a very important topic in ray optics and also the problems like this have to be solved using Snell’s law only. The refractive index of the air is equal to 1.